1.8. Электрическая энергия и мощность

В замкнутой электрической цепи под действием ЭДС постоянно происходит движение электрических зарядов.

. (53)

Работа, затраченная внешними силами на перемещение заряда Q в источнике или электрическая энергия источника

, (Дж). (54)

Так как Е = U + U_о,

то . (55)

То есть энергия, выработанная в источнике, расходуется на двух участках цепи.

Часть передается потребителю, а часть расходуется внутри самого источника.

Мощностью называется отношение работы А к времени t, в течение которого она выполнена,

, Вт (ватт). (56)

Мощность – это скорость, с которой совершается работа, или скорость, с которой происходит преобразование энергии.

Скорость, с которой механическая или другая энергия преобразуется в источнике питания в электрическую, называется мощностью источника (генератора):

, Вт. (57)

Скорость, с которой электрическая энергия преобразуется в другие виды энергии во внешнем участке цепи, называется мощностью потребителя (полезная мощность):

, Вт. (58)

Мощность, определяющая непроизводительные расходы электроэнергии в генераторе, называется мощностью потерь:

, Вт. (59)

По закону сохранения энергии

. (60)

Это выражение представляет собой баланс мощности электрической цепи.

Коэффициент полезного действия (КПД) цепи равен отношению полезной мощности (мощности потребителя) к затраченной мощности (мощности источника)

. (61)

Вопросы для самопроверки

1. В чем состоят первый и второй законы Кирхгофа?

2. Как рассчитывается эквивалентное сопротивление при последовательном соединении участков электрической цепи?

3. Как рассчитывается эквивалентная проводимость при параллельном соединении потребителей?

4. В чем заключается метод сворачивания электрической цепи?

5. Как преобразовать звезду в эквивалентный треугольник и обратно, треугольник в эквивалентную звезду?

6. На основании каких законов выводится метод узлового напряжения?

7. В чем отличие метода узловых и контурных уравнений от метода контурных токов?

Примеры решения задач

Пример 1. Определить токи во всех участках сложной цепи (рис. 11) методами:

контурных уравнений; преобразования и узлового напряжения; преобразования, узловых и контурных уравнений. Проверить правильность решения, составив баланс мощностей.

Дано: Е₁ = 120 В; Е₂ = 240 В; R₀₁ = R₀₂ = R₂ = 1 Ом; R₁ = R₄ = 6 Ом; R₃ = 4 Ом; R₅ = 10 Ом; R₆ = 8,8 Ом.

Определить: I₁…I₆.

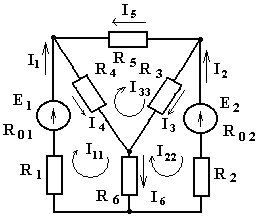
Рисунок 11

1. Решаем задачу методом контурных токов.

Алгоритм решения

1) Выбираем независимые контуры 11, 22,…,NN.

2) Произвольно выбираем направления токов в ветвях и направления обхода контуров (направления контурных токов).

3) Составляем контурные уравнения для контурных токов:

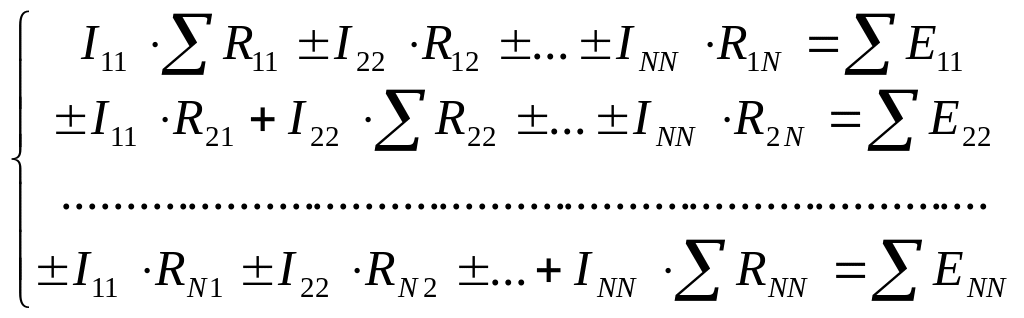,где

- контурные токи соответствующих контуров;

- суммарное сопротивление контуров 11, 22,…,NN соответственно;

- общее сопротивление смежных контуров;

- суммарная ЭДС контуров 11, 22,…, NN соответственно.

Знак «+» ставится перед контурными токами , если направления обхода в смежных контурах через общее сопротивление совпадает, и знак « - » - если направления обхода противоположны.

В суммарных ЭДС , ЭДС берется со знаком «+», если его направление совпадает с направлением обхода контура, и со знаком « - » - если его направление противоположно направлению обхода контура.

4) Решаем систему уравнений и определяем контурные токи.

5) Определяем токи в ветвях. Токи в ветвях, которые являются общими для двух контуров, определяются как алгебраические суммы соответствующих контурных токов. В остальных ветвях токи равны контурным токам.

Решение

Для схемы (рис.7) составляем контурные уравнения.

Подставляем численные значения

Решаем систему уравнений и находим контурные токи.

подставляем во 2-е уравнение

подставляем в первое уравнение

подставляем в 3-е ур-е

Определяем токи в ветвях: