Контрольная работа №2
Задача 1. На рис.54 показана трехфазная сеть, питающая две нагрузки, одна из которых соединена звездой, другая – треугольником. Система линейных напряжений симметрична (UAB = UBC = UCA = U).
Определить: фазные и линейные токи нагрузок; токи в проводах линии, питающей обе нагрузки; ток в нейтральном проводе; активную и реактивную мощности каждой из нагрузок и всей установки.
В масштабе построить векторную диаграмму токов и напряжений.
Задачу решить графо – аналитическим методом. Данные для своего варианта взять из таблицы 4.
Задача 2. К электрической цепи, состоящей из последовательно соединенных активного сопротивления R, индуктивности L, и емкости С, приложено несинусоидальное напряжение u = U0 + U1m·sinωt +U3m·sin3ωt.
Определить действующие значения несинусоидальных напряжения и тока, активную мощность и коэффициент мощности цепи, если частота первой гармоники f =50 Гц. Написать уравнение мгновенного значения тока цепи.
Данные для своего варианта взять из таблицы 5.
Примечание. Величины сопротивлений XL1 и XC1 округлять до целых чисел.
Задача 3. Для катушки со стальным сердечником, схема замещения которой представлена на рис.55, определить величину тока в катушке, подводимое переменное напряжение, мощность потерь в обмотке катушки и в стальном сердечнике. Параметры разветвленной схемы замещения приведены в таблице 6.
В масштабе постройте полную векторную диаграмму катушки.
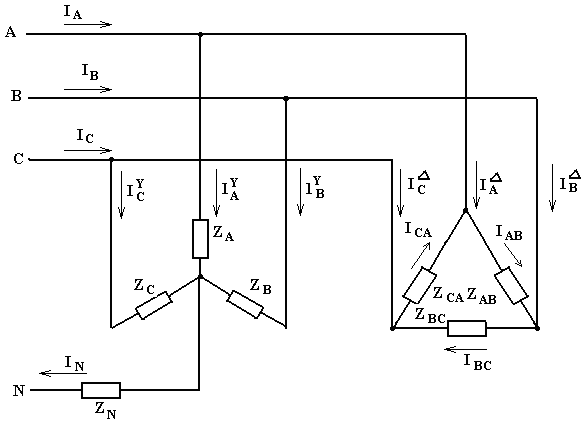
Рисунок 54
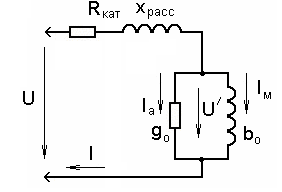
Рисунок 55
Таблица 4
Вари-анты |
U, B |
Приемник энергии, соединенный звездой |
Приемник энергии, соединенный треугольником |
|||||||
ZN, Ом |
Мощности фаз и коэффициент мощности |
Мощности фаз и коэффициент мощности |
||||||||
РА, Вт |
РВ, Вт |
РС, Вт |
cosφY |
РАВ, Вт |
РВС, Вт |
РСА, Вт |
cosφ∆ |
|||
1 |
380 |
0 |
2200 |
3300 |
4400 |
1 |
4607 |
4607 |
4607 |
0,866 |
2 |
380 |
∞ |
3872 |
3872 |
3872 |
0,8 |
5700 |
3800 |
7600 |
1 |
3 |
220 |
∞ |
1650 |
1650 |
1650 |
0,866 |
3300 |
5500 |
4400 |
1 |
4 |
220 |
0 |
1270 |
635 |
2540 |
1 |
2816 |
2816 |
2816 |
0,8 |
5 |
660 |
∞ |
1900 |
1900 |
1900 |
0,5 |
6600 |
3300 |
4620 |
1 |
6 |
380 |
0 |
2640 |
3300 |
2200 |
1 |
3230 |
3230 |
3230 |
0,5 |
7 |
220 |
0 |
2794 |
2540 |
3175 |
1 |
3300 |
3300 |
3300 |
0,6 |
8 |
660 |
∞ |
806 |
806 |
806 |
0,707 |
3960 |
2640 |
3300 |
1 |
9 |
380 |
∞ |
1980 |
1980 |
1980 |
0,6 |
4560 |
3800 |
3040 |
1 |
10 |
380 |
0 |
4400 |
3740 |
3300 |
1 |
5100 |
5100 |
5100 |
0,707 |
11 |
380 |
0 |
4400 |
3300 |
2200 |
1 |
4607 |
4607 |
4607 |
0,866 |
12 |
380 |
∞ |
3872 |
3872 |
3872 |
0,8 |
7600 |
3800 |
5700 |
1 |
13 |
220 |
∞ |
1650 |
1650 |
1650 |
0,866 |
4400 |
5500 |
3300 |
1 |
14 |
220 |
0 |
2540 |
635 |
1270 |
1 |
2816 |
2816 |
2816 |
0,8 |
15 |
660 |
∞ |
1900 |
1900 |
1900 |
0,5 |
4620 |
3300 |
6600 |
1 |
16 |
380 |
0 |
2200 |
3300 |
2640 |
1 |
3230 |
3230 |
3230 |
0,5 |
17 |
220 |
0 |
3175 |
2540 |
2794 |
1 |
3300 |
3300 |
3300 |
0,6 |
18 |
660 |
∞ |
806 |
806 |
806 |
0,707 |
3300 |
2640 |
3960 |
1 |
19 |
380 |
∞ |
1980 |
1980 |
1980 |
0,6 |
3040 |
3800 |
4560 |
1 |
20 |
380 |
0 |
3300 |
3740 |
4400 |
1 |
5100 |
5100 |
5100 |
0,707 |
Таблица 5
Варианты |
U, B |
R, Ом |
L, мГн |
С, мкФ |
1 |
u = 20 + 141·sinωt + 42,3·sin3ωt |
3 |
12,74 |
398 |
2 |
|
8 |
19,1 |
265,2 |
3 |
|
15 |
127,39 |
53 |
4 |
|
20 |
175,16 |
79,6 |
5 |
|
5 |
70,06 |
318,5 |
6 |
u = 30 + 225,6·sinωt + 70,5·sin3ωt |
16 |
54.14 |
637 |
7 |
|
24 |
41,4 |
530 |
8 |
|
12 |
28,66 |
796 |
9 |
|
6 |
25,48 |
199 |
10 |
|
30 |
79,62 |
354 |
11 |
u = 20 + 282·sinωt + 141·sin3ωt |
12 |
35 |
530 |
12 |
|
15 |
64 |
79,6 |
13 |
|
3 |
64 |
199 |
14 |
|
8 |
70 |
199 |
15 |
|
6 |
54,14 |
355 |
16 |
u = 30 + 70,5·sinωt + 42,4·sin3ωt |
4 |
19,2 |
354 |
17 |
|
10 |
60,5 |
796 |
18 |
|
4 |
28,6 |
530 |
19 |
|
4 |
25,5 |
637 |
20 |
|
12 |
79,62 |
354 |
Таблица 6
Вариант |
Rкат, Ом |
Xрасс, Ом |
g 0, См |
b 0, См |
U′, В |
1 |
2 |
3 |
0,047 |
0,2 |
70 |
2 |
1,5 |
2 |
0,009 |
0,072 |
100 |
3 |
1 |
2 |
0,05 |
0,1 |
65 |
4 |
2 |
4 |
0,04 |
0,15 |
80 |
5 |
1 |
1,5 |
0,075 |
0,3 |
60 |
6 |
1,67 |
2 |
0,03 |
0,09 |
90 |
7 |
1,59 |
2,65 |
0,06 |
0,1 |
110 |
8 |
2 |
4 |
0,08 |
0,11 |
55 |
9 |
1,32 |
1,24 |
0,045 |
0,25 |
50 |
10 |
1,46 |
1,7 |
0,01 |
0,08 |
75 |
11 |
4 |
6 |
0,094 |
0,4 |
140 |
12 |
3 |
4 |
0,018 |
0,144 |
200 |
13 |
2 |
4 |
0,1 |
0,2 |
130 |
14 |
4 |
8 |
0,08 |
0,3 |
160 |
15 |
2 |
3 |
0,15 |
0,6 |
120 |
16 |
3,34 |
4 |
0,06 |
0,18 |
180 |
17 |
3,18 |
5,3 |
0,12 |
0,2 |
220 |
18 |
4 |
8 |
0,16 |
0,22 |
110 |
19 |
2,64 |
2,48 |
0,09 |
0,5 |
100 |
20 |
2,92 |
3,4 |
0,02 |
0,16 |
150 |