6.2.2. Кривые, симметричные относительно оси ординат

Периодическая кривая называется симметричной относительно оси ординат, если любым двум абсциссам, имеющим одинаковое значение, но разные знаки, соответствуют ординаты, равные по величине и одинаковые по знаку, т.е. если кривая удовлетворяет уравнению:

. (151)

Кривая, симметричная относительно оси ординат, показана на рис. 37.

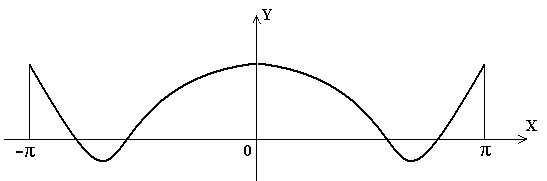
Рисунок 37

Кривые, симметричные оси ординат, не содержат синусоидальных составляющих:

. (152)

Кривую, симметричную относительно оси ординат имеет, например, кривая тока в нагрузке схемы однополупериодного выпрямления.

6.2.3. Кривые, симметричные относительно начала координат

Периодическая кривая называется симметричной относительно начала координат, если любым двум абсциссам, имеющим одинаковое значение, но разные знаки, соответствуют ординаты, равные по величине и обратные по знаку, т.е. кривая удовлетворяет уравнению:

. (153)

Кривая, симметричная относительно начала координат, показана на рис. 38.

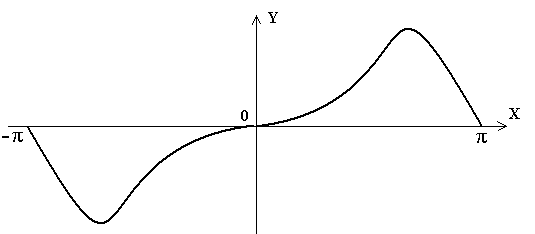
Рисунок 38

Кривые, симметричные относительно начала координат, не содержат постоянной составляющей и косинусоид:

. (154)

6.2.4. Кривые, симметричные относительно оси абсцисс и начала координат

Кривая, симметричная оси абсцисс и начала координат, показана на рис. 39.

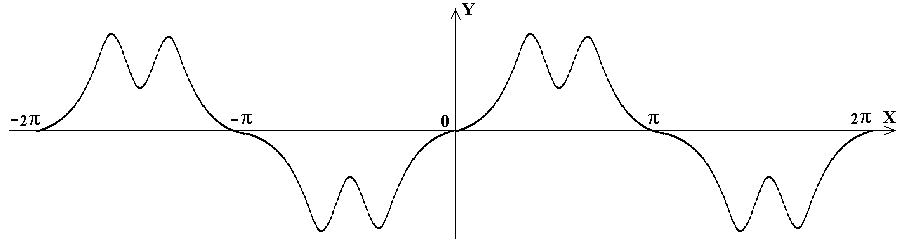
Рисунок 39

Кривые, симметричные оси абсцисс и начала координат, не содержат постоянной составляющей, четных гармоник и косинусоид, т.е. кривая удовлетворяет уравнению:

. (155)

6.3. Действующее значение несинусоидального тока

Действующее значение переменного синусоидального тока численно равно такому постоянному току, при котором выделяется столько же тепла, сколько его выделяется при переменном токе в одинаковом сопротивлении за одинаковое время, равное одному периоду Т. Из такого же условия определяется действующее значение переменного несинусоидального тока.

При этом нужно учесть, что несинусоидальный ток складывается из постоянной составляющей и ряда синусоидальных гармоник. Очевидно, общее количество тепла, которое выделяется при несинусоидальном токе, будет равно сумме количеств тепла от всех его составляющих.

Поэтому, действующее значение несинусоидального тока равно

, (156)

где I₀ – постоянная составляющая, а и т.д. – квадраты действующих значений синусоидальных составляющих.

Действующее значение несинусоидального напряжения равно

, (157)

где U₀ – постоянная составляющая, а и т.д. – квадраты действующих значений синусоидальных составляющих.

Действующее значение напряжений и токов не зависит от начальных фаз отдельных гармоник.

6.4. Расчет электрических цепей при несинусоидальном периодическом напряжении на входе

Расчет электрической цепи с несинусоидальными напряжениями выполняется на основе принципа наложения.

Источник несинусоидальной ЭДС можно представить как последовательное соединение источника постоянной ЭДС и источников синусоидальных ЭДС с соответствующими частотами.

Рассматривая действие каждого источника в отдельности, можно определить составляющие тока во всех участках цепи, выполняя расчет известными методами.

Значение тока в любом участке цепи равно алгебраической сумме значений токов от каждого источника.

Следовательно, расчет линейной цепи с несинусоидальными напряжениями сводится к решению нескольких задач: определение постоянной составляющей и ряда синусоидальных составляющих тока.

Решая эти задачи, нужно помнить, что реактивные сопротивления зависят от частоты. Поэтому для каждой гармонической составляющей нужно определить сопротивление цепи.

Сопротивления для k-й гармоники отличаются от сопротивления для первой в k раз:

(158)

Активное сопротивление считаем постоянным, равным сопротивлению постоянному току.

Активная мощность в цепи несинусоидального тока равна сумме активных мощностей, соответствующих постоянной составляющей и отдельным гармоникам:

. (159)

Реактивная мощность в цепи несинусоидального тока равна сумме реактивных мощностей соответствующих отдельным гармоникам:

. (160)

Полная мощность в цепи несинусоидального тока равна произведению действительных значений напряжения и тока:

S=U·I. (161)