3.3. Выражение синусоидальных величин комплексными числами
Если ток и
напряжение изменяются по синусоидальному
закону
,
(105)
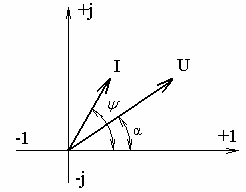
то их можно изобразить векторами (рис. 24.) и, следовательно, записать комплексными числами:
и
,
(106)
где
и
- комплексы
тока и напряжения.
Точка над комплексами указывает, что ток
Рисунок
24 и напряжение изменяются
по синусоидальному закону с определенной
частотой
;
I
и U
– модули комплексов тока и напряжения,
они же действующие значения тока
и напряжения
;
и
-
аргументы комплексов тока и напряжения,
они же начальные фазы тока
и напряжения
.
Закон Ома в комплексной форме
,
(107)
где
- комплекс
полного сопротивления
(комплексы величин, не зависящих от
времени, обозначаются большими буквами
с черточкой внизу).
Алгебраическая форма записи комплекса полного сопротивления
,
(108)
где
- активное
сопротивление;
- реактивное
сопротивление.
Обратная величина комплекса сопротивления – комплекс проводимости
,
(109)
где
- активная проводимость;
- реактивная
проводимость.
Любую цепь переменного тока можно рассчитывать по законам постоянного тока, если все величины представить в комплексной форме.
Комплекс
полной мощности цепи
определяется произведением комплекса
напряжения
и сопряженного комплекса тока
.
У сопряженного комплекса знак перед
мнимой единицей j
меняется на обратный
,
(110)
где
- вещественная часть комплекса полной
мощности –
активная мощность;
- коэффициент при
мнимой единице - реактивная
мощность;
- модуль комплекса
полной мощности
- кажущаяся
мощность;
- аргумент полной мощности – угол сдвига фаз между током и напряжением.
Расчет электрических цепей символическим методом
Геометрические операции над векторами можно заменить алгебраическими операциями над изображающими их комплексами, а все соотношения и законы постоянного тока применять к расчету цепей переменного тока.
В частности, при комплексной форме записи переменных токов и напряжений известные методы расчета цепей постоянного тока (метод контурных токов, метод наложения, метод узлового напряжения и др.) применимы и для расчета цепей переменного тока.
Законы Кирхгофа
Первый закон Кирхгофа. Алгебраическая сумма комплексов токов в узле равна нулю.
∑İ = 0 (111)
Второй закон Кирхгофа. В контуре электрической цепи алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов падений напряжений.
∑Ė = ∑İ
(112)
Метод узлового напряжения
Расчет схемы с двумя узлами может быть осуществлен определением узлового напряжения по формуле
(113)
Комплекс тока определяется по формуле
(114)
Правило выбора знаков ЭДС такое же, как и в цепях постоянного тока.