2.7Бинарные отношения.

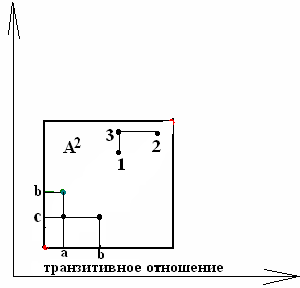
Говорят, что на множестве А задано (двуместное) отношение, если выделено некоторое подмножество ВÌ А². Говорят, что отношение В

1. рефлексивно., если "аÎА (а,а)ÎВ;

2. симметрично, если (а,b)ÎВ Þ (b,а)ÎВ;

3. антисимметрично, если (((а,b)ÎВ)Ù((b,а)ÎВ)) Þ (а=b);

4. транзитивно, если (((а,b)ÎВ)Ù ((b,с)ÎВ)) Þ ((а,с)ÎВ)

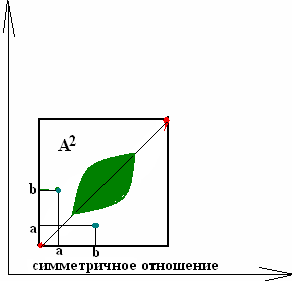Отношение называется отношением эквивалентности, если выполняются

первое, второе и четвёртое условия.

Отношение называется отношением (частичного) порядка, если выполняются первое, третье и четвёртое условия. Множество с заданным на нём отношением порядка называется частично упорядоченным. Если при этом к тому же выполняется условие "a,bÎM (aRb)Ú(bRa) то порядок R на множестве М называется линейным, а само множество М с заданным на нём отношением линейного порядка линейно упорядоченным (то есть тогда, когда любые два элемента М сравнимы между собой). Какие из вышеперечисленных четырёх условий выполняются для следующих множеств и отношений:

Упражнение 4.

1. М= множество людей на Земле. Отношение R между людьми: aRb если а дружит с b.

2. М= множество людей на Земле. Отношение R между людьми: aRb если а - родитель b.

3. М= множество N натуральных чисел. Отношение R таково: aRb если b делится на а.

4. М= множество N натуральных чисел. Отношение R таково: aRb если b=а+2.

5. М= множество N натуральных чисел. Отношение R таково: aRb если b=2а.

6. множество прямоугольников на плоскости. Отношение R таково: aRb если а и b имеют одинаковую площадь.

Упражнение 5.

Путь 1 означает наличие свойства, а 0 – его отсутствие. Упорядочим свойства рефлексивности, симметричности и транзитивности RST именно в этом порядке и сопоставим двоичной записи каждого числа от 0 до 7 соответствующую ей комбинацию наличия этих свойств. Так, например, 5₁₀=101₂ будет соответствовать отношению, которое рефлексивно, транзитивно, но не симметрично, а 2₁₀=10₂ будет соответствовать отношению, которое симметрично, но не рефлексивно и не транзитивно. Приведите примеры бинарных отношений на каждую комбинацию наличия или отсутствия этих трёх свойств.

число	RST	Множество и отношение в нём
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Индексы, знаки суммирования и произведения.

Когда мы работаем с небольшим количеством переменных, то мы их обозначаем разными буквами. Например, числа a, b, c или множества А, В, С или элементы этих множеств a, b, c, d, e, f, g,…Но если этих элементов много и само число этих элементов тоже неизвестно и может меняться, то что нам делать? Например, произвольное двузначное число можно обозначить как , где х – любая цифра, кроме 0, y-любая цифра. Но если речь идёт о 17-значном или 28-значном числе? Писать столько разных букв неудобно. Место много занимает. Ну, а если мы вообще не знаем, сколько в числе знаков? Число знаков само может быть переменной величиной.

Выход из положения нашли в том, чтобы использовать для названия однотипных объектов так называемые индексы – метки для букв. Например, вместо того, чтобы говорить об элементах a, b, c множества А, мы можем нумеровать буквы: первая, вторая, третья, говорить о первом, втором, третьем его элементах и обозначать их всех буквой а с номерком внизу (чтобы не спутать со степенями): a₁, a₂, a₃,…. В качестве «номерков» используют не только числа, но и элементы других множеств (иногда, например, элементов так много, что для их индексирования не хватает даже натуральных чисел!), так что индексы сами образуют множество – множество индексов. Запись А={a₁, a₂, a₃,…,a_n} означает, что множество А состоит из n элементов a₁,…, a_n. Например, при n=3 это значит, что А состоит из трёх элементов А={a₁, a₂, a₃}. Запись А= {a₁, a₂, a₃,…,a_n,…} или А={a₁, a₂, …} означает, что во множестве А бесконечно много элементов.

Теперь мы легко напишем произвольное число в его десятичной записи:

С индексированными переменными тесно связаны два других обозначения – для суммы и произведения n элементов. Если мы хотим найти сумму S всех элементов числового множества А={a₁, a₂, a₃,…,a_n}, то мы напишем S=a₁+a₂+a₃+…+a_n. Для сложения индексированных переменных используется символ , а для их умножения – символ . Внизу под этими знаками, ставится индекс (номер) первого переменного – с которого начинается операция суммирования или произведения, а вверху ставится индекс (номер) последнего переменного.

Так, вместо S=a₁+a₂+a₃+…+a_n можно написать : S= .

Если бы вместо сложения нам нужно было бы перемножить эти числа, то мы написали бы P=a₁a₂…a_n. Или, в сокращённой записи,: P= .

Например, пусть нам нужно сложить подряд числа, идущие подряд, начиная с 3 и кончая 11. В нашем примере а_i=i и 3+4+…+10+11=

Другой пример: пусть нужно перемножить все числа, кратные 3, начиная с 6 и кончая 39. Здесь а_i=3i и 69…39=

Здесь мы использовали для верхней границы произведения краткую запись: 13 вместо i=13.

Упражнение 6.

Запишите с помощью символов суммирования или произведения следующие суммы и произведения:

2²+3²+…+26²+27²

12+23+34+…+n(n-1)

6+10+14+18+...+102