48.Теорема Тейлора.
,
аналитическая внутри
,
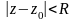может быть представлена в этом круге
степ.рядом
,
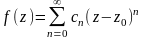причём он определён однозначно. □Выберем
,
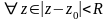построим окружность
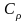с центром в
радиуса
.
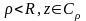Имеем
(*).
Преобразуем:
(**).
.
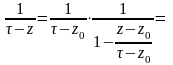
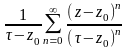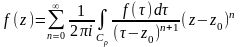
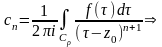по
теор. Коши можно заменить на
замкн.контур
,лежащим
в
.
,
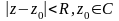аналитическая внутри
,
разлаг.в нём в сходящийся степ. ряд.
Коэф-ты разложения
.
Докажем ! разложения. Пусть есть другое:
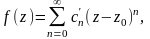где хотя бы один
.
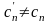Ряд сход-ся в
.
Из всего
.
?!?
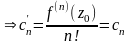! доказана. ■
49. Теоремы о нулях аналитической функции.
Пусть
f(z)
аналитична в окрестности т.
.
Для того что бы
была 0 функции кратности n
чтобы в некоторой окружности т.
f(z)
имела бы вид
,
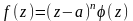где
,
f(z)
аналитична в U(
)
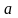I. Теорема о нулях аналитической функции.
Пусть а- ноль функции порядка f (z) аналитична в точке а,а в самой точке f (a) = 0 => f (z) 0 в U(a)
y a такая окрестность, где нет больше нулей, кроме точки а; нули аналитической функции изолированы
1) f (z)=
в
U(a)
f(a)
первый
коэф.
f
(a)=0=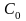
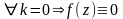в
U(a)
2)
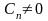f(z)
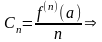a
– ноль порядка n
=>
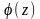-аналитична
в U(a)
U(a)
=> f(z)
f(z) нет других нулей кроме а
нули аналит. функции изолированы друг от друга
II. Теорема о нулях аналитической функции (следствие).
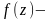аналитична
в
,
и
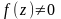в
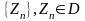
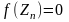
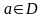
где
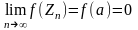а-ноль f(z)
но
начиная с некоторого №
много => не изолированный ноль =>
то
(по
I.
теор. о нулях)
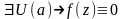
Замечание: Если в Т II типа не аналитичной обл.D , то это любая точка f(z)
50.Теорема Лорана.
(1)
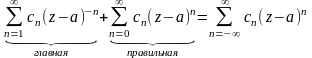
Ряд Лорана сх-ся, если сх-ся правильная и главная части.
Теорема. Если ряд Лорана сх-ся, то он сх-ся в некотором кольце.
f(z)=
Теорема
Лорана. Если f(z)-аналит.
в r<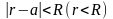
,
то f(z)=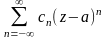
c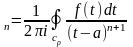
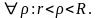
51.Неравенство Коши.
f(z)
огран. в r<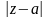
<R:
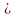M
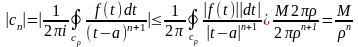
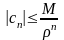-неравенство Коши
52.Классификация изолированных особых точек аналитической функции.
Опр.
Пусть f(z)-аналит.
: 0<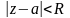
.Тогда
a-изолированная
особая точка f(z).
Классификация изолированных особых точек:
1.
a-устранимая
особая точка(у.о.т.), если
;
f(a)=A
2.
a-полюс:
;
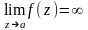a-полюс
f(z)
a-нуль
3.
a-существенно
особая точка(с.о.т.),
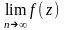
Пр.
1) f(z)=
,
z=0
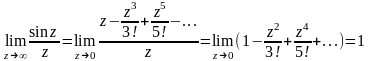f(z)={
2)
f(z)=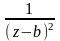
, b-полюс
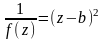
3)
f(z)=sin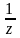
, z=0
не
f(z
=sin
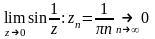
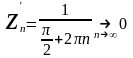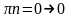f(z
53.Ряд Лорана в окрестности устранимой особой точки.
f(z)-аналит.
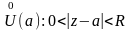
По
т.Лорана:f(z)=
Т.
a-у.о.т.
в
ряде Лорана в
)
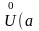отсутствует главная часть разложения.
Док-во:
Необходимость.
a-у.о.т.
:
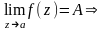в
)
.
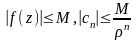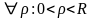
Достаточность.
f(z)=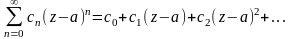
f(a)=c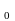
.
Конец.
Замечание.
У.о.т. будет, если в нек. окрестности
.
54.Ряд Лорана в окрестности полюса.
Т. (критерий полюса): a-полюс f(z) в главной части ряда Лорана для f(z) конечное число членов.
(Н)
a-полюс
f(z)
a-нуль
:
=
,
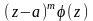0,
)
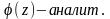f(z)=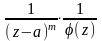
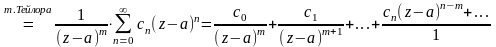
(Д)
f(z)=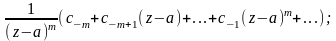
f(z)=
f(z)=
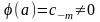
Опр.
a-полюс
f(z)
степень
m
для
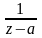наз-ся порядком полюса.Очевидно, если
a-нуль
порядка m
для
, то a-полюс
порядка m
для f(z).Очевидно,
a-полюс
f(z):
)
f(z)=
,
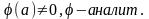
Пр.
f(z)=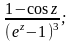
z=0;
Следствие. a-с.о.т. главная часть ряда Лорана содержала бесконечное число слагаемых.