26. Круговое свойство дробно-линейной функции.
W=az+b/cz+d ; - дробно-линейное отображение (a,b,c,d – комплексные числа) Теорема. При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая. □ w=a*z+b
рассмотрим: Это отображение сводится к подобию, повороту и переносу. Следовательно, окружности в окружности а прямые в прямые. При W=az+b/cz+d не линейной (коэфф С не нулевой) представим ее в виде W=A+B/z+z0 где A=a/c;B=(bc-ad)/c2 ; z0=d/c. Тогда отображение сводится к последовательному выполнению след отображений:
=z+z0
;
=1/
;
w=A+B
;
Первое и третье обладают круговым
свойством в силу линейности. Докажем
что и w=1/z
обладает этим свойством. Уравнение
любой окружности или прямой на комплексной
плоскости имеет вид
(x2+y2)+
x+
y+
=0;
(при
=0
это уравнение прямой) x2+y2=|z|2=z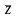
;
x=1/2(z+
);
y=1/2i(z-
);
уравнение теперь имеет вид
z
+Dz+
+
=0;
где D=1/2(
)
подставляем в w=1/z
и получаем
Следовательно
образом окружности (или прямой при
=0)
При отображении w=1/z является окружность (прямая при =0) ■ Отметим что W=az+b/cz+d переводит окружности и прямые, проходящие через z0=-d/c в прямые, а остальные окружности и прямые – в окружности. Прямай – это окружность бесконечного радиуса – следовательно все окружности переходят в окружности J
27. Принцип сохранения симметрии при дробно-линейном отображении.
Точки M и M* симметричные относительно окружности Г, если они лежат на одном луче, выходящем из O, и OM х OM*=R2; Каждая точка окружности симметрична сама себе относительно окружности. Теорема. При дробно-линейном отображении пара точек, симметричных относительно окр, переходят в пару точек, симметричных относительно образа этой окр. Здесь окружность может быть в частности и прямой. Чтобы доказать теорему надо сначала доказать лемму. Лемма: Точки M и M* являются симметричными тогда и тока тогда, когда любая - окружность, прох через точки, пересекается и Г под прямым углом.
□Необходимость.
Пусть M,
M*
симм относительно Г радиуса R
с центром в O.
Рассмотрим
проходящую через M
и M*,
проведем из O
прямую, касающуюся
в точке P.
Т.к. квадрат касательной равен произведению
секущей на ее внешнюю часть то OP2=OM
x
OM*.
Так как точки симметричны отн Г то OP=R,
следовательно окружности пересекаются
под прямым углом. ■ □Достаточность.
Любая окружность
проходящая через M
и M*
пересекается с Г под прямым углом, тогда
и любая прямая (частный случай окружности)
прох через две эти точки, тоже пересекает
Г под прямым углом. Значит прямая проходит
центр окружности O.
Более того, точки M
и M*
лежат на одном луче, выходящем из O,
так как в противном случае окружность
радиуса ½ MM*
не пересекала бы Г под прямым углом.
Докажем что OM
х OM*=R2
: Пусть окружности пересекаются в точке
P,
тогда OP
– касательная к
и OM
х OM*=R2
(по теореме о квадрате касательной) ■
Теперь имея лемму докажем Теорему о
симметрии □Пусть точки z
и z*
симметричны относительно Г и пусть
дробно-линейное отображение w=f(z)
переводит Г в
а
точки z
и z*
в точки w
и w*
соответственно. В силу кругового свойства
-
окружность. Нужно доказать что w
и w*
симм отн
.
Для этого в силу леммы достаточно
доказать что любая
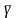прох через эти две
точки, пересекает
под прямым углом. Прообразом окружности
Является окружность прох через z и z* и эта окружность пересекает Г под прямым углом. Следовательно, и пересекаются тоже под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной компл плоскоти и сохраняет углы между кривыми в каждой точке! ■