
- •1. Свойства сходящихся числовых рядов
- •2. Критерий Коши сходимости числовых рядов. Необходимое условие сходимости
- •3. Признаки сравнения числовых рядов
- •5.Интегральный признак сходимости (Признак Коши - Маклорена)
- •4.Признак Коши и Даламбера
- •7. Признак Лейбница для знакочередующихся рядов
- •6. Абсолютно и условно сходящиеся ряды.
- •8. Признак Дирихле-Абеля
- •9. Перестановка членов сходящихся рядов.
- •12.Признаки Вейерштрасса и Дирихле
- •1) Теорема (достаточное условие равномерной сходимости функциональных рядов (Вейерштрасса)):
- •13. Непрерывность суммы рсфр
- •15. Почленное дифференцирование рсфр
- •14. Почленное интегрирование рсфр
- •16.Предел последовательности комплексных чисел. Необходимое и достаточное условия.
- •17.Кривые и области комплексной плоскости. Основные определения.
- •20.Основные элементарные фкп
- •21.Дифференцирование фкп. Условия Коши-Римана.
- •22.Условия Коши-Римана в полярных кординатах.
- •23.Теорема о сопряженной гармонической функции.
- •24.Геометрический смысл производной гармонической функции.
- •25.Общие свойства конформных отображений.
- •26. Круговое свойство дробно-линейной функции.
- •27. Принцип сохранения симметрии при дробно-линейном отображении.
- •28. Конформное отображение дробно-линейной функцией:
- •29. Конформные отображения элементарными функциями (z2,zn, √z, n√ z).
- •37.Теорема Морера.
- •38.Принцип максимума модуля.
- •39.Теорема Лиувилля.
- •40.Основная теорема алгебры
- •41.Равномерная сходимость рядов фкп.
- •42.Непрерывность суммы равномерно сходящихся рядов фкп.
- •43. Почленное интегрирование равномерно сходящихся рядов фкп.
- •46. Теорема Абеля.
- •47.Круг и радиус сходимости степенного ряда.
- •48.Теорема Тейлора.
- •49. Теоремы о нулях аналитической функции.
- •I. Теорема о нулях аналитической функции.
- •53.Ряд Лорана в окрестности устранимой особой точки.
- •54.Ряд Лорана в окрестности полюса.
- •55.Теорема Сохоцкого.
- •56. Вычисление вычетов аналитической функции.
- •57. Основная теорема теории вычетов.
- •58. Вычисление определенных интегралов с помощью теории вычетов.
- •59. Теорема единственности.
- •60.Аналитическое продолжение г-функции.
1. Свойства сходящихся числовых рядов
1°.
Пусть ряд
 сходится и
сходится и
 Тогда для любого
Тогда для любого
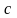 (
= const)
сходится ряд
(
= const)
сходится ряд
 и имеет сумму
и имеет сумму
 .
{Пусть
.
{Пусть
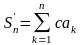 .
. ,
,
 }.
}.
2°.
Если сходятся
ряды
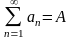 и
и
 ,
то сходится ряд
,
то сходится ряд
 и имеет сумму A+B.
и имеет сумму A+B.
{Пусть
 .
=>
.
=>
 }.
}.
3°.
Если
 ,
то для любых чисел
,
то для любых чисел
 и
и

 .{Следует
из 1° и 2°}
.{Следует
из 1° и 2°}
4°. Если сходится ряд , то сходится и любой его остаток. Если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
{Обозначим
m-ый
остаток ряда
 ,
его p-ую
частичную сумму
,
его p-ую
частичную сумму
 .
Пусть
.
Пусть
 .
.
 ;
;
 (*) Зафиксируем
(*) Зафиксируем
 ,
а
,
а
 устремим к бесконечности. Тогда
устремим к бесконечности. Тогда
 .
.
 и остаток ряда
сходится.
и остаток ряда
сходится.
Если
же известно, что сходится остаток ряда
 ,
то из (*) следует:
,
то из (*) следует:
 и ряд
сходится.
и ряд
сходится.
Обозначим
 .
Тогда из (*) следует:
.
Тогда из (*) следует:
 (**) или
(**) или
 .}
.}
Выводы:
1. Переходя
в (**) к пределу при
 ,
получаем
,
получаем
 2.Отбрасывание
конечного числа начальных членов ряда
или присоединение в начале его нескольких
новых членов не отражается на поведении
ряда (в смысле его сходимости или
расходимости).
2.Отбрасывание
конечного числа начальных членов ряда
или присоединение в начале его нескольких
новых членов не отражается на поведении
ряда (в смысле его сходимости или
расходимости).
2. Критерий Коши сходимости числовых рядов. Необходимое условие сходимости
Теорема
(критерий Коши): Для
того чтобы ряд
сходился,
необходимо и достаточно, чтобы и
и
 выполнялось бы:
выполнялось бы:
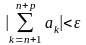 .
{Сходимость
числового ряда определяется сходимостью
числовой последовательности {
.
{Сходимость
числового ряда определяется сходимостью
числовой последовательности { }.
Ранее доказано: для того чтобы
последовательность {
}
сходилась, необходимо и достаточно,
чтобы
}.
Ранее доказано: для того чтобы
последовательность {
}
сходилась, необходимо и достаточно,
чтобы
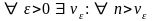 и
выполнялось бы:
и
выполнялось бы:
 или
или
 .}
.}
Теорема
(необходимое условие сходимости) :
 .
Переходя к пределу при
,
получим:
.
Переходя к пределу при
,
получим:
 .
Тот же результат можно получить из
критерия Коши, полагая p
= 1. Очевидно, условие
является необходимым, но не достаточным
условием сходимости числового ряда.
(НО : Ряд
.
Тот же результат можно получить из
критерия Коши, полагая p
= 1. Очевидно, условие
является необходимым, но не достаточным
условием сходимости числового ряда.
(НО : Ряд
 расходится , однако
расходится , однако
 )
)
3. Признаки сравнения числовых рядов
Теорема
1 (признак сравнения): Пусть
даны два ряда:
 (1) и
(1) и
 (2). Если, начиная с некоторого номера
выполняется:
(2). Если, начиная с некоторого номера
выполняется:
 (3),
(3),
 ,
то из сходимости ряда (2)
,
то из сходимости ряда (2)
 сходимость ряда (1); из расходимости ряда
(1)
расходимость ряда (2).
сходимость ряда (1); из расходимости ряда
(1)
расходимость ряда (2).
{Не
ограничивая общности, будем считать,
что неравенство
выполняется для всех n
. Пусть
 .
Очевидно, последовательности {
.
Очевидно, последовательности { }
и {
}
и { }
– монотонные неубывающие. Пусть ряд
(2) сходится. Тогда {
}
ограничена:
}
– монотонные неубывающие. Пусть ряд
(2) сходится. Тогда {
}
ограничена:
 .
Но тогда, в силу (3),
.
Но тогда, в силу (3),
 и ряд (1) – также сходится.
и ряд (1) – также сходится.
Пусть ряд (1) расходится. Если бы ряд (2) сходился, то, по доказанному выше, сходился бы и ряд (1). Т.е. получили бы противоречие. Таким образом, ряд (2) также расходится.}
Теорема
2 (признак сравнения в предельной форме):
Пусть
 Если существует
Если существует
 то ряды (1) и (2) сходятся либо расходятся
одновременно.
{ Пусть ряд
(2) сходится.
Из существования
то ряды (1) и (2) сходятся либо расходятся
одновременно.
{ Пусть ряд
(2) сходится.
Из существования
 :
:
 ,
откуда получаем:
,
откуда получаем:
 или
или
 следует сходимость ряда (1).
Пусть ряд
(2) расходится.
Существует
следует сходимость ряда (1).
Пусть ряд
(2) расходится.
Существует
 ,
откуда аналогичным образом получаем:
,
откуда аналогичным образом получаем:
 .
Если бы сходился ряд (1), а вместе с ним
и ряд
.
Если бы сходился ряд (1), а вместе с ним
и ряд
 ,
то по теореме 1 сходился бы и ряд (2). А
это не так. Значит, ряд (1) также расходится.}
,
то по теореме 1 сходился бы и ряд (2). А
это не так. Значит, ряд (1) также расходится.}
 .
Так как
.
Так как
 ,
а ряд
,
а ряд
 - расходится (
- расходится ( то расходится и ряд
то расходится и ряд
 .
.
5.Интегральный признак сходимости (Признак Коши - Маклорена)
Теорема
(Коши - Маклорена): Пусть
функция у = f(x)
определена при х≥1, неотрицательна и
монотонно убывает на
 ∞).
Тогда ряд
∞).
Тогда ряд
 ,
где
,
где
 сходится
тогда и только тогда, когда сходится
несобственный интеграл
сходится
тогда и только тогда, когда сходится
несобственный интеграл
 (2)
(2)
[Так
как f(x)
монотонна на
∞) , то она интегрируема по Риману на
любом отрезке [1, ],
поэтому имеет смысл
],
поэтому имеет смысл
 .
Так как f(x)-убывает
на
∞), то для
.
Так как f(x)-убывает
на
∞), то для
 f(k+1)
f(k+1)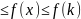 .
Проинтегрируем последнее неравенство
по отрезку
.
Проинтегрируем последнее неравенство
по отрезку
 :
:
 ,
k=1,2,3.4...
,
k=1,2,3.4...
Просуммируем по к:
 Обозначим ,
Обозначим ,
 Тогда
Тогда

Пусть несобственный
интеграл (2) сходится. Последовательность
 монотонна (
монотонна (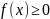 )
и ограничена. Тогда ограничена и
последовательность
)
и ограничена. Тогда ограничена и
последовательность
 .
А поскольку она монотонно возрастает,
то является сходящейся.
.
А поскольку она монотонно возрастает,
то является сходящейся.
Пусть сходится
ряд (1). Покажем, что сходится несобственный
интеграл (2). Последовательность
 – монотонная, сходящаяся последовательность,
следовательно, ограничена.
– монотонная, сходящаяся последовательность,
следовательно, ограничена.
Тогда из (3) следует
ограниченность возрастающей
последовательности
,
а следовательно, её сходимость. То есть
существует конечный
 ;
интеграл (2) сходится. }
;
интеграл (2) сходится. }
Пример :
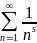 ,
s>0,
Рассмотрим
f(x)=
,
s>0,
Рассмотрим
f(x)=
 на [1,
на [1, );
);

Значит,
ряд сходится при s
>1 и расходится при s
