11. Тройной интеграл в сферических координатах.

Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где 

ρ − длина радиуса-вектора точки M; φ − угол, образованный проекцией радиуса-вектора   на плоскость Oxy и осью Ox;θ − угол отклонения радиуса-вектора   от положительного направления оси Oz (рисунок 1).

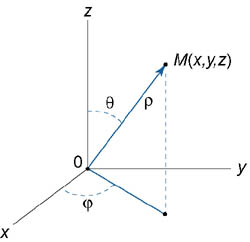
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.  Сферические координаты точки связаны с ее декартовыми координатами соотношениями

Якобиан перехода от декартовых координат к сферическим имеет вид:

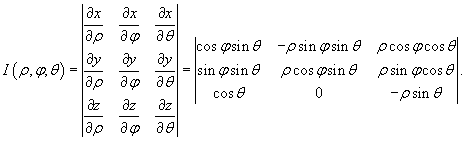
Раскладывая определитель по второму столбцу, получаем

Соответственно, абсолютное значение якобиана равно

Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:

Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования Uпредставляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет видf (x² + y² + z²).  Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами

В этом случае якобиан равен

12.Механические приложения тройного интеграла.

Пусть μ(x, y, z) — объемная непрерывная плотность тела V. Тогда:масса тела V

статические моменты относительно координатных плоскостей:

центр масс тела:

,  ,  моменты инерции относ.коорд.плоск.

,  относительно координатных осей

,  ,  относительно начала координат

13. Криволинейный интеграл I рода. Основные свойства кри-I.

Обобщением определенного интеграла на случай, когда область интегрирования есть некоторая кривая, является так называемый криволинейный интеграл.

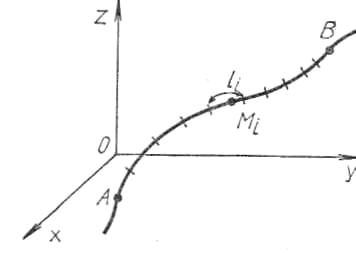Дугу произвольным образом разобьем на n n частей .Пусть длина каждой дуги ddf равна , . На каждой дуге вавапвап выберем произвольную точку aaaaaaaaaaaaaaaaaaaa . Составим интегральную смссм сумму . Пусть ,  наибольшая из длин дуг деления.Пусть в пространстве ( ) задана гладкая дуга кривой , во всех точках которой определена непрерывная функция .Если при , когда , существует конечный предел интегральной суммы , то его называют криволинейным интегралом первого рода (КРИ-I) или криволинейным интегралом по длине дуги от функции , и обозначается .

Таким образом, по определению

. (2.1)

Если кривая лежит в плоскости и вдоль этой кривой задана непрерывная функция , то .

Надо отметить, если функция непрерывная в каждой точке гладкой кривой, то криволинейный интеграл I рода существует, и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.

Основные свойства КРИ-I

1. , т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования.

2. , где .

3. .

4. , если путь интегрирования разбить на части и такие, что , и имеют единственную общую точку.

5. Если для точек кривой выполняется неравенство , то .

6. Если , то , где  длина кривой (геометрический смысл криволинейного интеграла первого рода).

7. (Теорема о среднем) Если функция непрерывная на кривой , то на этой кривой найдется точка , что .

Некоторые приложения криволинейного интеграла II рода

Площадь плоской фигуры

Площадь плоской фигуры, расположенной в плоскости и ограниченной замкнутой линией , можно найти по формуле

,при этом кривая , делает обход против часовой стрелки.

Работа переменной силы

Переменная сила на криволинейном участке производит работу, которая находится по формуле

.