
- •2.Вычисление двойного нтеграла в декартовых координатах.
- •5. Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
- •7. Механические приложения двойного интеграла.
- •8. Определение и свойства тройного интеграла.
- •4)Если в области r,то ;
- •5)Если в области r и , то ;
- •6)Если на r и области r и s являются непересекающимися , то . Здесь означает объединение этих двух областей.
- •10.Вычисление тройного интеграла в цилиндрических координатах
- •11. Тройной интеграл в сферических координатах.
- •12.Механические приложения тройного интеграла.
- •13. Криволинейный интеграл I рода. Основные свойства кри-I.
- •14.Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Формула Остроградского – Грина.
- •16.Приложения кри(1-2)
- •17.Поверхностный интеграл 1-го рода
- •18.Поверхностный интеграл II рода.
- •19.Формула Стокса
- •20. Пови-2 по замкнутым поверхностям. Формула Астроградского.
- •21.Понятие скалярного поля. Поверхности и линии уровня.
- •22.Производная скалярного поля по направлению. Градиент.
- •23. Понятие векторного поля. Векторные линии векторного поля.
- •24.Циркуляция и ротор векторного поля.
- •25.Поток и дивергенция векторного поля.
- •26.Оператор Гамильтона и некоторые его применения.
- •27.Потенциальное,соленоидальное и гармоническое векторные поля.
- •28.Понятие числового ряда и его суммы. Свойства числовых рядов.
- •29.Необходимый признак сходимости ряда.
- •30.Интегральный признак Коши.
- •31.Признак сравнения рядов с положительными членами.
- •32.Признак Даламбера.
- •33.Радикальный признак Коши
- •34.Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •35.Знакочередующиеся ряды. Признак Лейбница.
- •36.Функциональные ряды. Свойства правильно сходящихся рядов.
- •37.Степенные ряды. Область сходимости.
- •38.Свойства степенных рядов.
- •39.Ряды Тейлора и Маклорена.
8. Определение и свойства тройного интеграла.
Теория тройного интеграла аналогична теории двойного интеграла.
Рассмотрим в
пространстве
![]() замкнутую
область
замкнутую
область
![]() .
Пусть в области
задана непрерывная функция
.
Пусть в области
задана непрерывная функция
![]() .1)
Разбиваем область
на
.1)
Разбиваем область
на
![]() «элементарных областей»
«элементарных областей»
![]() .2)
Объем «элементарной области»
.2)
Объем «элементарной области»
![]() обозначим
обозначим
![]() ,
а диаметр (наибольшее расстояние между
двумя точками области) – через
,
а диаметр (наибольшее расстояние между
двумя точками области) – через
![]() .3)Возьмем
произвольную точку
.3)Возьмем
произвольную точку
![]() .4)
Находим
.4)
Находим
![]() .5)
Составляем интегральную сумму
.5)
Составляем интегральную сумму
![]() .
.
6) Обозначим через
![]() длину наибольшего из диаметров
«элементарных областей», т.е.
длину наибольшего из диаметров
«элементарных областей», т.е.
![]() ,
,
![]() .
Найдем предел интегральной суммы, когда
.
Найдем предел интегральной суммы, когда
![]() так, что
так, что
![]() .
.
![]() .
.
Предел интегральной
суммы, когда число «элементарных
областей» неограниченно возрастает, а
длина наибольшего диаметра стремится
к нулю, называется тройным
интегралом от
на замкнутой областью
.Таким
образом, тройным
интегралом от
по замкнутой областью
называется предел интегральной суммы
![]() ,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
![]() .
интегрируемая
функция в
области
;
.
интегрируемая
функция в
области
;
область
интегрирования;![]() ,
,
![]() и
и
![]()
переменные
интегрирования;
переменные
интегрирования;
![]() или
или
![]()
элемент
объема.
элемент
объема.
Свойства
1) 2)
3) , где k –
константа;
4)Если в области r,то ;
5)Если в области r и , то ;
6)Если на r и области r и s являются непересекающимися , то . Здесь означает объединение этих двух областей.
9.
Вычисление тройного интеграла в
декартовых координатах.Пусть
функция 3-х переменных u = f (x, y, z)
задана и непрерывна в замкнутой области
V![]() xOyz.
Тройной интеграл от этой функции по
области V имеет вид:
xOyz.
Тройной интеграл от этой функции по
области V имеет вид: ![]() ,
где
,
где ![]() .Если
область V – правильная в направлении
оси Oz (рис. 5), то ее можно задать системой
неравенств:
.Если
область V – правильная в направлении
оси Oz (рис. 5), то ее можно задать системой
неравенств: ![]() где
z = z1 (x, y) и z = z2 (x, y)
– это уравнения поверхностей,
ограничивающих область (тело) V
соответственно снизу и сверху (рис.
5). Если область D можно задать системой
неравенств
где
z = z1 (x, y) и z = z2 (x, y)
– это уравнения поверхностей,
ограничивающих область (тело) V
соответственно снизу и сверху (рис.
5). Если область D можно задать системой
неравенств![]() то
то ![]() В
этом случае тройной интеграл от функции
u = f (x, y, z) по области V можно
вычислить при помощи трехкратного
повторного интеграла:
В
этом случае тройной интеграл от функции
u = f (x, y, z) по области V можно
вычислить при помощи трехкратного
повторного интеграла:![]() .Здесь
каждый внутренний интеграл вычисляется
по «своей» переменной интегрирования
в предположении, что переменные
интегрирования внешних интегралов
остаются постоянными.Существует всего
6 вариантов сведения тройного интеграла
к трехкратному в декартовых координатах
(в зависимости от выбранного порядка
интегрирования).Вычисление тройного
интеграла в цилиндрических
координатахЦилиндрические координаты
точки М в пространстве – это ее полярные
координаты на плоскости xOy и координата
z, т.е.
.Здесь
каждый внутренний интеграл вычисляется
по «своей» переменной интегрирования
в предположении, что переменные
интегрирования внешних интегралов
остаются постоянными.Существует всего
6 вариантов сведения тройного интеграла
к трехкратному в декартовых координатах
(в зависимости от выбранного порядка
интегрирования).Вычисление тройного
интеграла в цилиндрических
координатахЦилиндрические координаты
точки М в пространстве – это ее полярные
координаты на плоскости xOy и координата
z, т.е. ![]() .Преобразование
тройного интеграла по области V к
цилиндрическим координатам осуществляется
при помощи формул
.Преобразование
тройного интеграла по области V к
цилиндрическим координатам осуществляется
при помощи формул ![]() ,
, ![]() ,
, ![]() :
: ![]() .Если
область V задана системой неравенств:
.Если
область V задана системой неравенств:![]() причем
причем ![]() то
V:
то
V: ![]() Вычисление
тройного интеграла по области V в
цилиндрических координатах сводится
к вычислению трехкратного интеграла в
соответствии с записанной системой
неравенств для области V:
Вычисление
тройного интеграла по области V в
цилиндрических координатах сводится
к вычислению трехкратного интеграла в
соответствии с записанной системой
неравенств для области V:![]() .
.
10.Вычисление тройного интеграла в цилиндрических координатах
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
П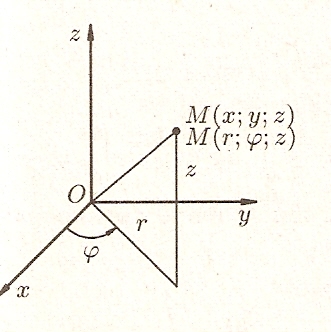 оложение
точки
оложение
точки
![]() в пространстве
можно определить заданием трех числе
в пространстве
можно определить заданием трех числе
![]() ,
где
,
где
![]()
длина радиус-вектора проекции точки
длина радиус-вектора проекции точки
![]() на плоскость
на плоскость
![]() ,
,
![]()
угол, образованный этим радиус-вектором
с осью
угол, образованный этим радиус-вектором
с осью
![]() ,
аппликата точки
(см. рис.).
,
аппликата точки
(см. рис.).
Три числа
![]() называются цилиндрическими
координатами
точки
.Цилиндрические
координаты точки связаны с ее декартовыми
координатами следующими соотношениями:
называются цилиндрическими
координатами
точки
.Цилиндрические
координаты точки связаны с ее декартовыми
координатами следующими соотношениями:
![]() ,
,
![]() ,
,![]() ,где
,где
![]()
![]() .
.
Возьмем в качестве
![]() цилиндрические координаты
и вычислим якобиан преобразования:
цилиндрические координаты
и вычислим якобиан преобразования:
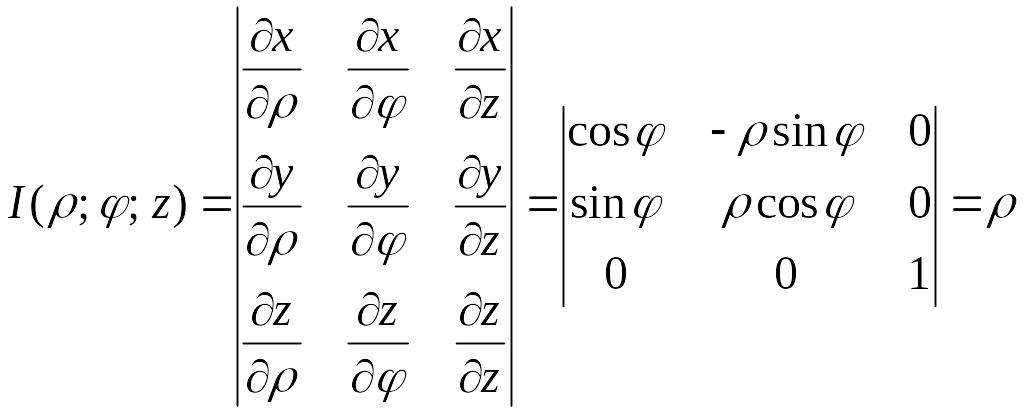 .
.
Формула замены переменных (1.9) принимает вид:
![]() .
.
Таким образом, вычисление тройного интеграла приводится к интегрированию по , по , по аналогично тому, как это делается в декартовых координатах. К цилиндрическим координатам бывает удобно перейти, если область интегрирования образована цилиндрической поверхностью.
