30.Интегральный признак Коши.

Теорема 5.7 (интегральный признак Коши). Пусть дан ряд

,

члены которого являются значениями непрерывной положительной функции при целых значениях аргумента :

,

и пусть монотонно убывает на промежутке . Тогда ряд сходится, если сходится несобственный интеграл , и расходится, если несобственный интеграл расходится.Надо отметить, что вместо интеграла можно брать интеграл , где . Отбрасывание первых членов ряда, как известно, не влияет на сходимость (расходимость) ряда.

31.Признак сравнения рядов с положительными членами.

Пусть даны два знакоположительных ряда:

 и 

.Тогда, если, начиная с некоторого места (n > N), выполняется неравенство:

,то из сходимости ряда   следует сходимость  .Или же, если ряд  расходится, то расходится и  .

Также этот признак удобно записывть в виде отношений:

Если для членов строго положительных рядов   и  , начиная с некоторого места (n > N), выполняется неравенство: ,

то из сходимости ряда   следует сходимость  , а из расходимости   следует расходимость  .

Передельный признак сравнения

Поскольку достоверно установить справедливость этого неравенства при любых n — довольно сложная задача, то на практике признак сравнения обычно используется в предельной форме.

Если   и   есть строго положительные ряды и

,то при   из сходимости   следует сходимость  , а при   из расходимости   следует расходимость  .

Вариант 2

Сходимость или расходимость числовых рядов с положительными членами часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.

Теорема 5.3. Пусть даны два ряда с положительными членами:

и

Если для всех выполняется неравенство , то

1. из сходимости ряда (5.9) следует сходимость ряда (5.8);

2. из расходимости ряда (5.8) следует расходимость ряда (5.9).

Надо отметить, что теорема 5.3 справедлива и в том случае, когда неравенство выполняется не для всех членов рядов (5.8) и (5.9), а начиная с некоторого номера . Это вытекает из свойства 3 числовых рядов.

Теорема 5.4 (предельный признак сравнения). Пусть даны два ряда (5.8) и (5.9) с положительными членами. Если существует конечный, отличный от нуля, предел

где , то ряды (5.8) и (5.9) сходятся или расходятся одновременно.

32.Признак Даламбера.

В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами.

Теорема 5.5 (признак Даламбера). Пусть дан ряд (5.1) с положительными членами и существует конечный или бесконечный предел

.

Тогда:

1. при 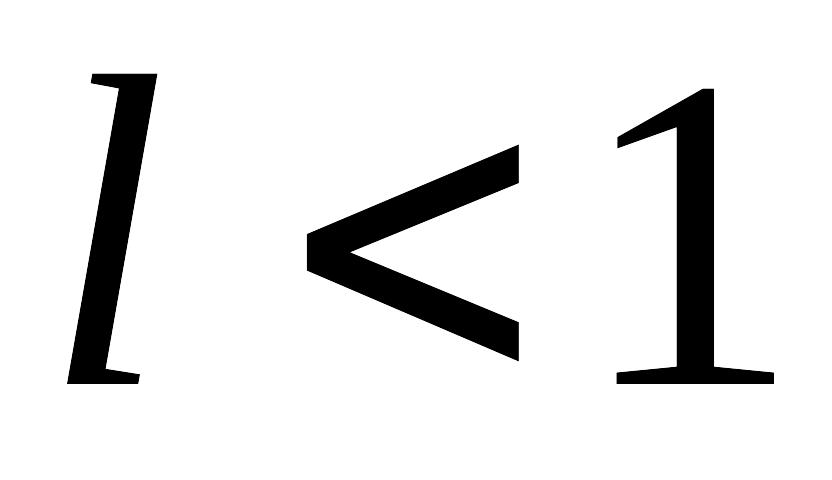ряд сходится;

2. при 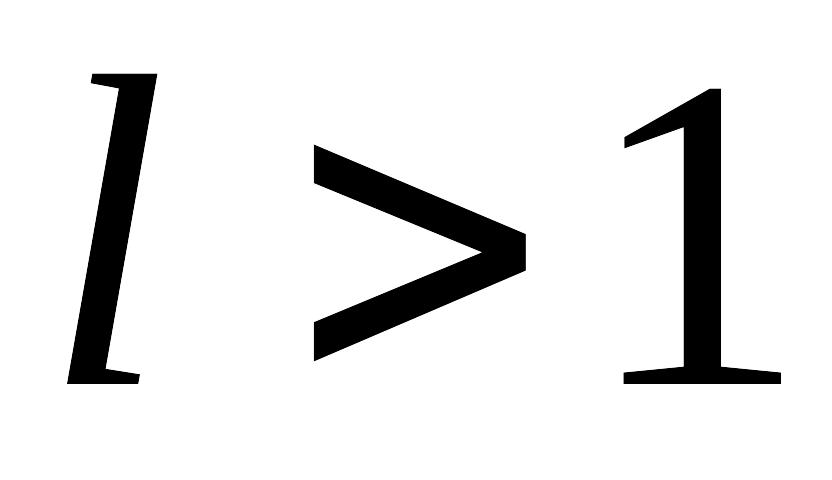ряд расходится.

При признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.

Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида или .