
- •2.Вычисление двойного нтеграла в декартовых координатах.
- •5. Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
- •7. Механические приложения двойного интеграла.
- •8. Определение и свойства тройного интеграла.
- •4)Если в области r,то ;
- •5)Если в области r и , то ;
- •6)Если на r и области r и s являются непересекающимися , то . Здесь означает объединение этих двух областей.
- •10.Вычисление тройного интеграла в цилиндрических координатах
- •11. Тройной интеграл в сферических координатах.
- •12.Механические приложения тройного интеграла.
- •13. Криволинейный интеграл I рода. Основные свойства кри-I.
- •14.Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Формула Остроградского – Грина.
- •16.Приложения кри(1-2)
- •17.Поверхностный интеграл 1-го рода
- •18.Поверхностный интеграл II рода.
- •19.Формула Стокса
- •20. Пови-2 по замкнутым поверхностям. Формула Астроградского.
- •21.Понятие скалярного поля. Поверхности и линии уровня.
- •22.Производная скалярного поля по направлению. Градиент.
- •23. Понятие векторного поля. Векторные линии векторного поля.
- •24.Циркуляция и ротор векторного поля.
- •25.Поток и дивергенция векторного поля.
- •26.Оператор Гамильтона и некоторые его применения.
- •27.Потенциальное,соленоидальное и гармоническое векторные поля.
- •28.Понятие числового ряда и его суммы. Свойства числовых рядов.
- •29.Необходимый признак сходимости ряда.
- •30.Интегральный признак Коши.
- •31.Признак сравнения рядов с положительными членами.
- •32.Признак Даламбера.
- •33.Радикальный признак Коши
- •34.Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •35.Знакочередующиеся ряды. Признак Лейбница.
- •36.Функциональные ряды. Свойства правильно сходящихся рядов.
- •37.Степенные ряды. Область сходимости.
- •38.Свойства степенных рядов.
- •39.Ряды Тейлора и Маклорена.
26.Оператор Гамильтона и некоторые его применения.
Основными дифференциальными операциями (действиями) над скалярным полем и векторным полем являются: градиент, дивергенция, ротор. Эти действия называются векторными операциями первого порядка (в них участвуют только производные первого порядка).
Векторные операции
– нахождение градиента, дивергенции,
ротора, удобно описывать с помощью
дифференциального оператора, который
обозначается символом
![]() (читается «набла») и называется оператором
Гамильтона:
(читается «набла») и называется оператором
Гамильтона:
![]() .
.
Он приобретает
смысл лишь в комбинации со скалярными
или векторными функциями. Символическое
«умножение» вектора
на скаляр
или вектор
производится по обычным правилам
векторной алгебры, а «умножение» символов
![]() на величины
,
на величины
,
![]() ,
,
![]() ,
понимают как взятие соответствующей
частной производной от этих величин.
,
понимают как взятие соответствующей
частной производной от этих величин.
Выразим основные дифференциальные операции с помощью оператора Гамильтона:
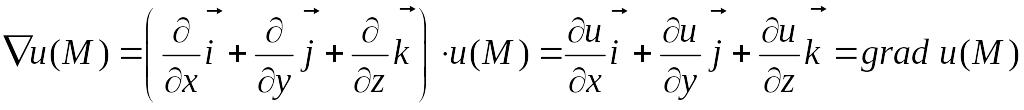 .
. .
.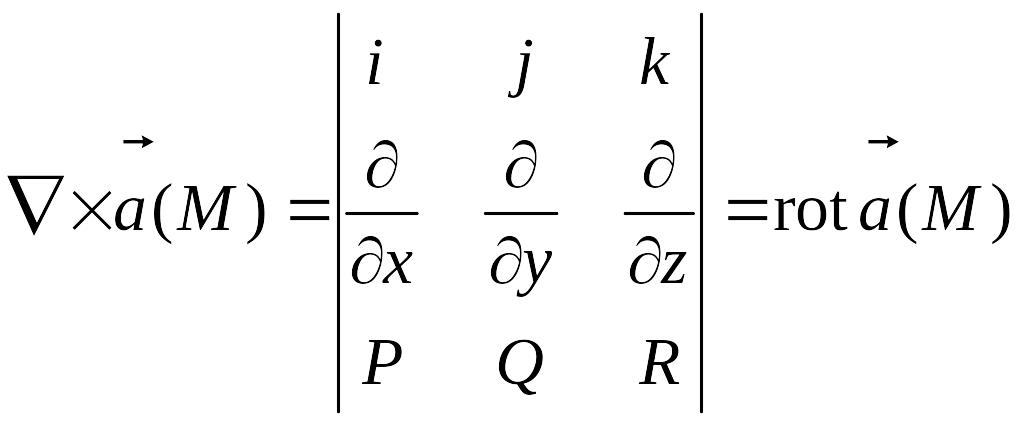 .
.
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действии с ними надо пользоваться правилами векторной алгебры и правилами дифференцирования.
После применения
оператора Гамильтона к скалярному или
векторному полю получается новое поле,
к которому можно снова применит этот
оператор. В результате получаются
дифференциальные
операции второго порядка.
Можно убедиться, что имеется лишь пять
дифференциальных операций второго
порядка:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Понятно, что, например, операция
.
Понятно, что, например, операция
![]() не имеет смысла, так как
не имеет смысла, так как
![]()
есть скаляр.
есть скаляр.
Дифференциальный оператор
![]()
также называется оператором Гамильтона.
Запишем основные дифференциальные операции второго порядка, используя оператор Гамильтона:
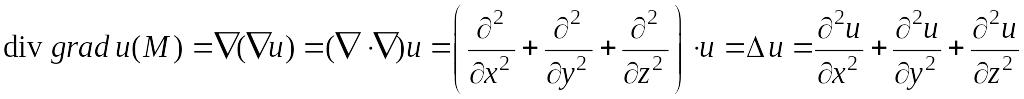 .
.
Таким образом, получаем дифференциальное уравнение
![]() ,
,
которое называется дифференциальным уравнением Лапласа. Это уравнение играет важную роль в различных разделах математической физике. Решениями уравнения Лапласа являются так называемые гармонические функции.
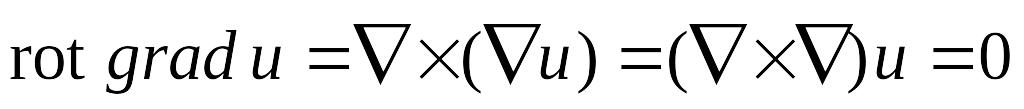 ,
так как векторное произведение двух
одинаковых векторных полей равно
нулевому вектору. Это означает, что
поле градиента есть поле безвихревое.
,
так как векторное произведение двух
одинаковых векторных полей равно
нулевому вектору. Это означает, что
поле градиента есть поле безвихревое.
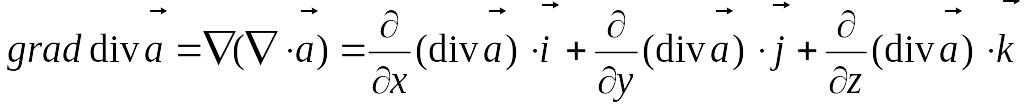 .
.
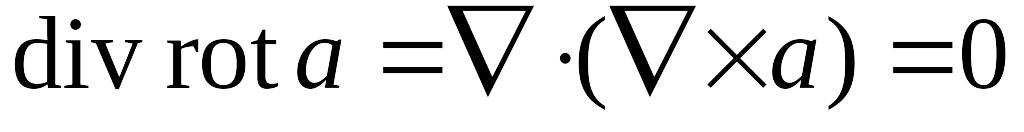 ,
так как смешанное произведение трех
векторов, из которых два одинаковых,
равно нулю.
,
так как смешанное произведение трех
векторов, из которых два одинаковых,
равно нулю.
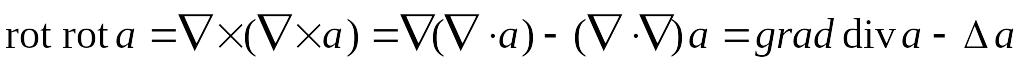 .
.
27.Потенциальное,соленоидальное и гармоническое векторные поля.
Соленоидальное векторное поле
Векторное поле называется соленоидальным или трубчатым в области , если в каждой точке этой области .
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие.
Приведем некоторые свойства соленоидального поля:
В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю. Соленоидальное поле не имеет источников и стоков.
Соленоидальное поле является полем ротора некоторого векторного поля, т.е. если , то существует такое поле
 ,
что
,
что
 .
Вектор
называется векторным
потенциалом
поля
.
.
Вектор
называется векторным
потенциалом
поля
.
Так как
![]() ,
то поле ротора любого векторного поля
является соленоидальным.
,
то поле ротора любого векторного поля
является соленоидальным.
3. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение, называемое интенсивностью трубки.
Потенциальное векторное поле
Векторное поле называется потенциальным или безвихревым, или градиентным в односвязной области , если в каждой точке этой области
.
Примером потенциального поля является электрическое поле напряженности точечного заряда и другие.
Приведем некоторые свойства потенциального поля:
Циркуляция потенциального поля по любому замкнутому контуру в этом поле равна нулю.
В частности, для
силового потенциального поля это
означает, что работа силы по любому
замкнутому контуру равна нулю. В поле
скоростей текущей жидкости равенство
![]() означает, что в потоке нет замкнутых
струек, т.е. нет водоворотов.
означает, что в потоке нет замкнутых
струек, т.е. нет водоворотов.
В потенциальном поле криволинейный интеграл
 вдоль любой кривой
с началом в точке
вдоль любой кривой
с началом в точке
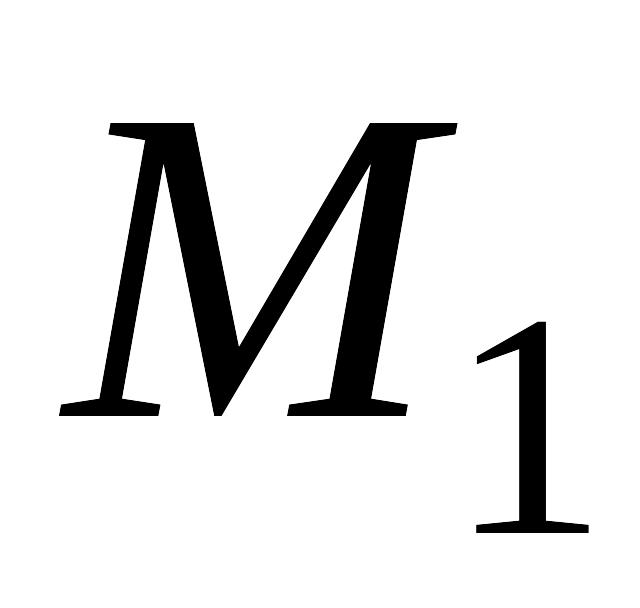 и концом в точке
и концом в точке
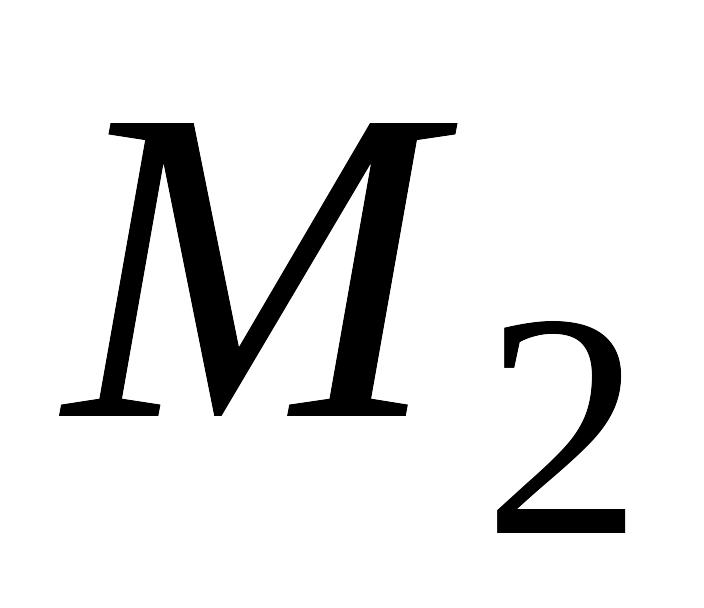 зависит только от положения точек
и
,
и не зависит от формы кривой.
зависит только от положения точек
и
,
и не зависит от формы кривой.Потенциальное поле является полем градиента некоторой скалярной функции
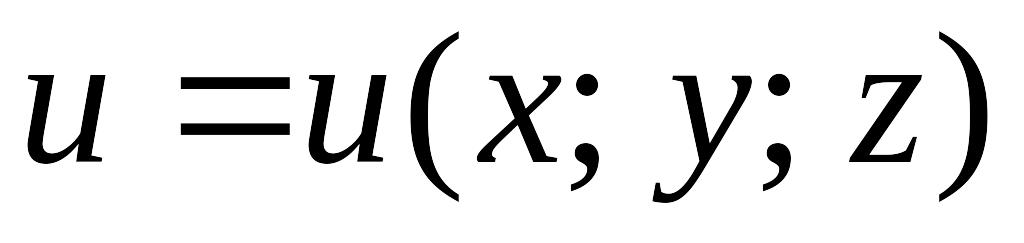 ,
т.е. если
,
т.е. если
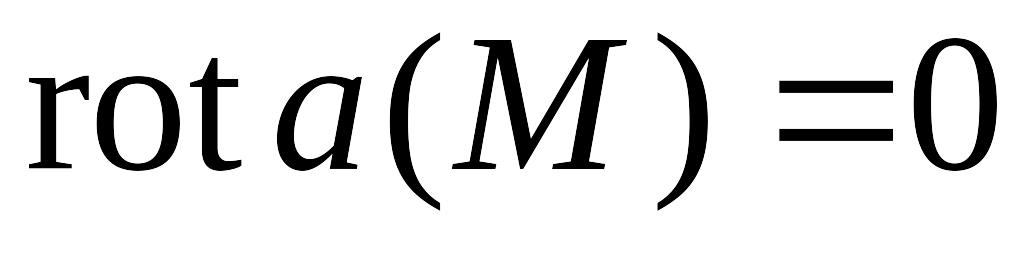 ,
то существует функция
такая, что
,
то существует функция
такая, что
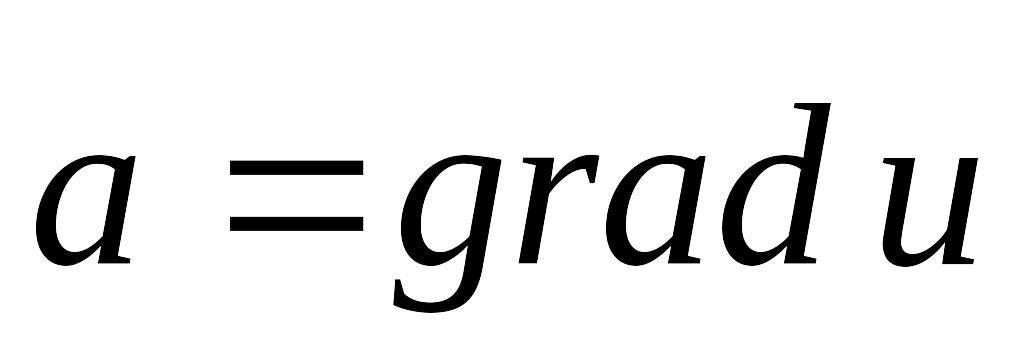 .
.
Из равенства
![]() следует обратное утверждение: поле
градиента скалярной функции
является потенциальным.
следует обратное утверждение: поле
градиента скалярной функции
является потенциальным.
Для того чтобы поле было потенциальным в области , необходимо и достаточно, чтобы существовала дважды непрерывно дифференцируемая скалярная функция , такая, что , которая называется потенциальной функцией (потенциалом) поля .
Потенциал векторного поля можно найти по следующей формуле:
![]() ,где
,где
![]()
некоторая фиксированная точка области
,
любая точка области
,
произвольная постоянная.
некоторая фиксированная точка области
,
любая точка области
,
произвольная постоянная.
Гармоническое векторное поле
Векторное поле называется гармоническим или лапласовым, если оно одновременно является потенциальным и соленоидальным, т.е. если
и .
Примером гармонического
поля является поле линейных скоростей
стационарного безвихревого потока
жидкости при отсутствии в нем источников
и стоков.Потенциал
гармонического поля является решением
уравнения Лапласа![]() .
.
Функция , удовлетворяющая уравнению Лапласа, называется гармонической.
