1.Определение и свойства двойного интреграла. Назовем диаметром области D_i точную верхнюю грань расстояний между двумя любыми точками этой области. Символом  обозначим наибольший из диаметров частичных областей D₁, D₂, ..., D_r.Число I называется пределом интегральных сумм (3) при  , если для любого положительного числа ε можно указать такое положительное число δ, что при   независимо от выбора точек P_i в частичных областях D_i выполняется неравенство Общее определение интегрируемости. Функция f(x, y) называется интегрируемой (по Риману) в области D, если существует конечный предел I интегральных сумм   этой функции при  . Указанный предел называется двойным интегралом от функцииf(x, y) по области D. Свойства двойного интеграла:Двойной интеграл обладает следующими свойствами:

1) 2)

3) , где k –

константа;

4)Если   в области R,то  ;

5)Если   в области R и  , то  ;

6)Если   на R и области R и S являются непересекающимися , то  .  Здесь   означает объединение этих двух областей.

2.Вычисление двойного нтеграла в декартовых координатах.

Покажем, что вычисление двойного интеграла сводится к последовательному в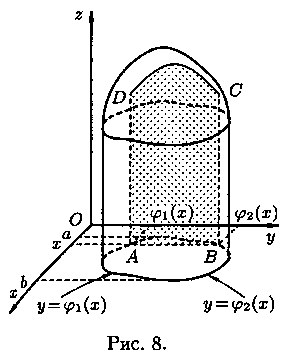 ычислению двух определенных интегралов.Пусть требуется вычислить двойной интеграл   где функция ƒ(х;у)>=0 непрерывна в области D. Тогда, как это было показано в п. 7.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z=ƒ(х;у). Найдем этот объем, используя метод параллельных сечений. Ранее (см. Часть 1, ( 41.6)) было показано, что где S(x) - п лощадь сечения плоскостью, перпендикулярной оси Ох, a x=a,x=b - уравнения плоскостей, ограничивающих данное тело.Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=₁(x) и у=₂(х), причем функции ₁(x) и ₂(х) непрерывны и таковы, что ₁(x) ≤ ₂(х) для всех х є [а;b] (см. рис. 7). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х =const, где х є [а; b].В сечении получим криволинейную трапецию ABCD, ограниченную линиями z=ƒ(х;у), где х=const, z=0, у=₁(x) и у=₂(х) (см. рис. 8). Площадь S(х) этой трапеции находим с помощью определенного интеграла Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть  найден

так:

С другой стороны, в п. 7.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции ƒ(х;у) >=0 по области D. Следовательно, Это равенство обычно записывается в виде Формула (7.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (7.7) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.При этом    называется внутренним интегралом.Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.Если же область D ограничена прямыми y=c и y=d(c<d), кривыми x=Ψ₁(у)и х=Ψ₂(у)> причем Ψ₁(у)≤Ψ₂(у) для всех у є [с;d], т. е. область D - правильная в направлении оси Ох, то, рассекая тело плоскостью у=const, аналогично получим: Здесь, при вычислении внутреннего интеграла, считаем у постоянным.

3.Двойной интеграл в полярных координатахДля упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.Определим преобразование независимых переменных х и у (замену переменных) как Если функции (7.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция ƒ(х;у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:

Функциональный определитель (7.10) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7.11) не приводим.Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и .В качестве u и υ возьмем полярные координаты r и . Они связаны с декартовыми координатами формулами х=rcos , у=r sin  (см. Часть 1, п. 9.1).Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (7.10) как Формула замены переменных (7.11) принимает вид: где D* - область в полярной системе координат, соответствующая области D в декартовой системе координат.Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область D* имеет вид, изображенный на рисунке 10 (ограничена лучами =а и =β, где а < β, и кривыми r=r₁() и r=r₂(), где r₁()≤r₂(), т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (7.12) можно  записать в виде

Внутренний интеграл берется при постоянном .

Замечания.Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ƒ(х²+у²); область D есть круг, кольцо или часть таковых. На практике переход к полярным координатам осуществляется путем замены х=rcos , у=rsin , dxdy=r dr d; уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по r и  (исследуя закон изменения r и  точки (r; ) при ее отождествлении с точкой (х; у) области D).

4Двойной интеграл в криволинейных координатахПусть двойной интеграл преобразуется от прямоугольных координат {x, y} к криволинейным координатам {u,v}, связанным с прямоугольными координатами соотношениями x = x(u, v), y = y(u, v), где функции x(u, v) и y(u, v), имеют непрерывные частные производные в области D^/ плоскости uO^/v и якобиан преобразования в области D^/ не обращается в нуль:  (102)При этом устанавливается взаимнооднозначное и в обе стороны непрерывное соответствие между точками области D плоскости хОу и точками области D^/плоскости uO^/v (рис. 11)

Рис. 11

Формула преобразования двойного интеграла в этом случае имеет вид

. (103)

В частности, для полярных координат

. (104)