10. Основной закон динамики.

П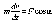 усть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол  с каса­тельной а окружности (рис. 26).

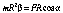
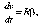
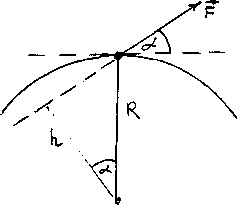
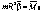
Rcos=h (плечо силы относительно центра окружности).

Следовательно, величина mR² определяет инертные свойства тела при вращатель­ном движении. Эта величина I=mR² называется моментом инер­ции тела (точки). С учетом сказанного основной закон динамики для вращательного движения записывают в виде:

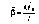
1 1. Движение тел в поле центральных сил.

Центральными называют силы, линии действия которых проходят в своё время через один и тот же центр. Примером таких сил могут служить силы гравитационного взаимодействия между планетами Солнечной системы.

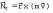
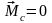
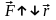
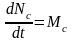
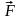
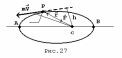
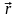Основные особенности движения тел в поле центральных сил рассмотрим на примере движения планеты вокруг Солнца. Планета Р (рис.27) движется вокруг Солнца, центр масс которого находится в точке с. Радиус-вектор планеты , а сила, действующая на неё со стороны Солнца - . Движение планеты вокруг Солнца описывается уравнением моментов:

Т.к.. , следовательно:

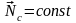Постоянство вектора означает постоянство как его модуля, так и направления в пространстве. Из

у 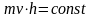словия постоянства направления следует, что орбита планеты плоская, т.е. она движется всё время в одной и той же плоскости.

И з условия постоянства модуля вектора следует, что:

Считая массу планеты постоянной, можно далее записать:

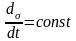Из рисунка видно, что h*dS равно удвоенной площади, ометаемой радиус-вектором планеты за промежуток времени dt.Обозначив эту площадь dσ, получим:

т.е. площадь, ометаемая радиус-вектором планеты в единицу времени (секториальная скорость) постоянна.

12. Основной закон динамики системы материальных точек.

. Системой материальных точек (механической системой) называют совокупность взаимодействующих между собой точек, в которой положение и движение каждой из них зависит от положения и движения остальных точек системы (например, Солнечная планетная система).

Для любой точки системы (например, k-й) можно записать основной закон динамики Ньютона в виде:

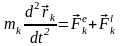
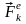
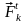
где ― равнодействующая внешних сил, приложенных к k-й точке системы, ― равнодействующая внутренних сил, приложенных к k-й точке.

Записав таким образом уравнения динамики по второму закону для всех точек системы и суммируя их, получаем:

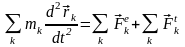
У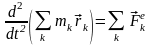 читывая, что геометрическая сумма внутренних сил равна нулю, имеем:

С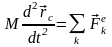 учётом (2-31) можно окончательно записать основной закон динамики для системы материальных точек в виде, аналогичном основному закону динамики для материальной точки:

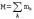
где: ― общая масса системы.