49. Сложение одинаково направленных колебаний. Частоты складываемых колебаний одинаковы.

Предположим, что точка одновременно принимает участие в двух гармонических движениях вдоль одного и того же направления, при этом частоты складываемых колебаний равны между собой, отличаются только амплитуды и начальные фазы колебани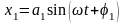й:

и

По принципу суперпозиции колебаний полное смещение точки из положения равновесия должно быть равным геометрической сумме смещений, получаемых в каждом из отдельных колебаний. Кроме того, поскольку оба составляющих колебания происходят с одной и той же частотой, то и результирующее колебание будет иметь ту же частоту. Поэтому результат сложения колебаний представим в виде функции:

Используя формулы для тригонометрических преобразований, далее запишем, что:

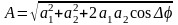
Амплитуда результирующего колебания может принимать различные значения в зависимости от значений амплитуд складываемых колебаний и разности их начальных фаз. Например, если фазы складываемых колебаний отличаются на 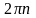, то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А = а₁ + а_г если же разность фаз равна (2п + 1) , то - разности амплитуд А = а₁-а_г. При разности фаз, равной нечётному числу амплитуда результирующего колебания равна .

50. Частоты складываемых колебаний различны, одинаковы амплитуды и начальные фазы

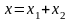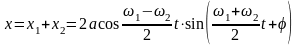При складывании колебаний различных частот равенство амплитуд и начальных фаз мы взяли только для упрощения преобразований. Пусть первое из складываемых колебаний имеет вид , а второе- . По принципу суперпозиции колебаний . Используя формулы тригонометрических преобразований, получаем результат в виде: (339)

Как видно, результирующее колебание в этом случае не является гармоническим. Однако, если частоты складываемых колебаний не очень отличаются друг от друга, то результирующее колебание можно представить как почти гармоническое с медленно изменяющейся амплитудой. При этом смещение точки из положения равновесия происходит с частотой, равной полусумме складываемых частот. Такой случай сложного колебания называется биениями, т.е. периодическими изменениями амплитуды результирующего колебания, возникающие при сложении двух одинаково направленных гармонических колебаний с близкими частотами. Частота биений при этом определяется разностью частот складываемых колебаний .

Пусть складываемые колебания имеют, разные амплитуды, а начальные фазы для простоты рассуждений будем считать одинаковыми:

и .

Результирующее колебание будем определять по принципу суперпозиции, несколько преобразовав складываемые колебания:

.

Первые два члена в этом выражении в результате дают биения. Таким образом, амплитуда результирующего колебания (биений) не обращается в нуль, а уменьшается только до величины, равной разности амплитуд складываемых колебаний. Примерный вид биений при сложении колебаний с одинаковыми и различными амплитудами приведен на рис.106 и рис.107.