44. Собственные колебания

Основные особенности собственных колебаний рассмотрим на примере механической колебательной системы с одной степенью свободы, т.е. такой системы, положение которой можно в любой момент времени определять только одной координатой. Будем счи­тать, что размеры тела достаточно малы, чтобы его можно было рассматривать как материальную точку. Предположим, что при выводе тела из положения равновесия на него будут действовать силы, пропорциональные смещению и направленные противоположно этому смещению -kx. Как говори­лось выше, трением, сопротивлением среды можно пренебречь. Внутренние же силы, величина и направление которых определя­ются смещением из положения равновесия, могут быть, например, силами упругости или силами другой природы, но изменяющимися так же, как и упругие . Такие силы, независимо от их природы, будем называть 'квазиупругими'. С учётом этих сил дифференциальное уравнение движения принимает вид

Решением дифференциального уравнения движения (314) имеет вид гармонической функции

Как видно, равенство будет соблюдаться для любого момен­та времени, если:

Действительно, отношение можно представить в виде квадрата некоторой величины, поскольку масса тела, коэффициент упругости и, следовательно, само отношение положительны. Как коэффициент k , так и масса тела являются внутренними парамет­рами колебательной системы, поэтому циклическая частота коле­баний  не зависит от начальных условий. От начальных условий зависит только амплитуда колебаний и начальная фаза, которые можно найти из начальных условий, как это было показано ранее. Скорость и ускорение тела при собственных колебаниях так­же изменяются по гармоническому закону:

45. Затухающие колебания

Выясним теперь характер колебаний рассмотренной системы при наличии трения. При этом будем полагать, что силы трения пропорциональны скорости тела и противоположно ей направлены. Такими силами, например, являются силы вязкого трения при до­статочно малых скоростях движения тела. Если тело выведено из положения равновесия на величину x и при этом имеет скорость , то на него будут действовать квазиупругая сила F=-kx и сила сопротивления движению , где,  - коэффициент сопротивления. По второму закону динамики напишем дифференциаль­ное уравнение движения

Введём обозначения и . C учётом этих обозначений дифференциальное уравнение принимает вид

Строгое решение этого уравнения рассматривается в теории дифференциальных уравнений. Это же решение можно получить, исходя из следующих соображений. Во-первых, наличие квазиупру­гих сил свидетельствует о том, что в системе, выведенной из положения равновесия, должны возникнуть колебания. Во-вторых, наличие сил сопротивления движению приводит к тому, что энер­гия колебательной системы и, следовательно, амплитуда колебаний с течением времени должны уменьшаться, кроме того, сопро­тивление среды, тормозя движение тела, влияет на быстроту ко­лебаний, т.е. циклическая частота колебаний может зависеть от сопротивления среды. Исходя из сказанного, решение уравнения будем искать в виде

Если выражение действительно является решением урав­нения, то после подстановки в мы должны получить тождество:

Очевидно, тождество будет выполняться для любого произ­вольного момента времени, если будут выполняться следующие условия

Из условия получаем дифференциальное уравнение для определения амплитуды колебаний

Разделяя переменные, получаем уравнение, удобное для ин­тегрирования

Решением этого уравнения является функция ,

где А₀ - постоянная интегрирования, которую можно определить из начальных условий. Подставив найденное значение амплитуды колебаний в условие , получаем:

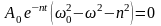
т.е. частота колебаний действительно отличается от частоты собственных колебаний и равна:

Период колебаний соответственно равен:

С учётом полученных результатов решение исходного диффе­ренциального уравнения движения записывается в виде:

Это и есть закон колебаний при наличии вязкого трения. Такие колебания называются затухающими.

Скорость и ускорение колебаний тела при наличии вязкого трения определяются соотношениями

Рассмотренные колебания являются периодическими (все параметры движения изменяются по периодическому закону). В то же время затухающие колебания нельзя назвать гармоническими. Об этом свидетельствует уже зависимость от времени амплитуды колебаний. К тому же выводу приводит и более подробный анализ периодичности изменения отдельных параметров движения, например смещения и скорости. Действительно, из выражений для смещения и скорости сле­дует, что моменты времени, соответствующие прохождению телом положения равновесия, отвечают условию:

а моменты обращения в нуль скорости тела – условию:

Из этих условий следует, что прохождение телом положения равновесия и обращение в нуль скорости тела происходит с оди­наковым периодом. Однако промежутки времени между прохожде­нием положения равновесия и последующим обращением в нуль ско­рости тела не равны четверти периода, как это имеет место при гармонических колебаниях. Следовательно, и по этой причине затухающие колебания не могут быть гармоническими. Степень "негармоничности" затухающих колебаний определяется величиной коэффициента .

Таким образом, в рассмотренном случае затухания колебаний амплитуда убывает с течением времени по геометрической прогрес­сии. Быстрота затухания колебаний определяется величиной по­терь энергии колебаний (величиной коэффициента сопротивления движению). Кроме того, с увеличением коэффициента сопротивления уменьшается не только амплитуда колебаний, но и частота, а пе­риод колебаний, соответственно, увеличивается. Следует также отметить, что колебания не могут продолжаться бесконечно дол­го, как это можно было бы предположить из закона колебаний. Дело в том, что когда амплитуда колебаний становится беско­нечно малой, малыми будут и упругие силы. При определённых ус­ловиях они не смогут преодолеть сопротивления движению и ко­лебания прекратятся. При достаточно больших коэффициентах со­противления среды процесс затухания колебаний вплоть до полного их прекращения протекает очень быстро. Может получиться, что система не сможет совершить даже одного полного колебания.

Т акие колебания называют апериодическими. На практике же коле­бания считают прекратившимися при уменьшении амплитуды колеба­ний до некоторой заданной доли начального значения амплитуды (обычно до 1%). Графически затухающие колебания и апериодически процесс представлены на рис. 82 и рис.83.

При колебаниях системы в вязкой среде, когда силы сопро­тивления движению пропорциональны первой степени скорости, амплитуда колебаний убывает с течением времени по геомет­рической прогрессии, а отношение амплитуд колебаний, отстоящих друг от друга ни один период колебаний, остаётся с тече­нием времени постоянным и равным:

Т аким образом, величину этого отношения можно взять в ка­честве характеристики затухания колебаний, её называют декре­ментом затухания. Натуральный логарифм этого отношения (назы­вается логарифмическим декрементом затухания)

Эту важную характеристику затухающих колебаний на прак­тике берут по абсолютному значению, без учёта его знака. Знак "-" физически означает, что с течением времени амплитуда коле­баний уменьшается.

В реальных механических колебательных системах затухание стремятся свести к минимуму, затухание при этом становится настолько малым, что уменьшением амплитуды колебаний за один период можно пренебречь. Уменьшение амплитуды становится за­метным только через достаточно большой промежуток времени.

Все полученные количественные результаты относительно рассмотренных затухающих колебании справедливы только при на­личии вязкого трения. Если же в системе на колеблющееся тело действуют силы сухого трения, то при сохранении качественных выводов (например, амплитуда колебаний с течением времени уменьшается) количественные характеристики будут иными, будет иным и сам характер изменения амплитуды) колебаний.