27. Закон всемирного тяготения.

Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид:

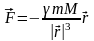
где - масса источника гравитационного поля, 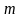- величина пробной массы, 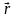-радиус-вектор точечной пробной массы относительно центра масс источника поля, - гравитационная постоянная.

Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля:

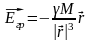
Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”,”тяжёлые” или ”гравитационные” массы.

28.Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал.

Потенциальная энергия взаимодействия численно равна работе сил взаимодействия по перемещению взаимодействующего тела из данного положения в бесконечность:

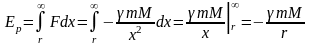
Энергетической характеристикой поля является гравитационный потенциал, равный потенциальной энергии единичной пробной массы, помещённой в данную точку поля:

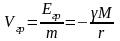
Связь напряжённости и потенциала поля.

На расстояниях 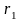и 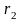от источника поля напряжённости поля равны: 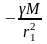и

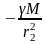
В этих же точках определим потенциалы: и

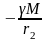
Изменение потенциала на еденицу длинны:

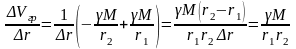
Если точки расположены бесконечно близко друг к другу, связь напряжённости и потенциала принимает вид:

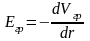
29. Работа силы, работа суммы сил.

Работой силы называют величину, равную произведение силы на перемещение точки приложения силы:

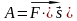
Как видно, если сила и перемещение взаимно перпендикулярны, работа силы равна нулю. Например, центростремительная сила не производит работы, ее роль сводится лишь к искривлению траектории.

Работа суммы сил равна сумме работ, производимых отдельными силами системы. Например:

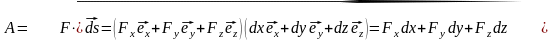
Работа силы тяжести.

Пусть тело под действием силы тяжести скользит по наклонной поверхности произвольной формы работа нормальной реакции по равна нулю, поэтому при отсутствии трения работу совершает только сила тяжести. На элементарном перемещении работа силы равна:

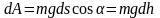
Следовательно, на конечном перемещении работа сил тяжести не зависит от формы траектории и равна:

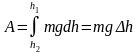
где: 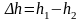перемещение тела по вертикали.

Работа упругих сил.

На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости с вертикальной стенкой .

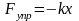Если под действие внешней силы пружина растягивается на , возникает сила упругости пружины, равная в пределах упругих деформаций . Элементарная работа упругих сил по перемещению тела из этого положения на 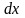равна:

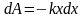
Работа же силы на конечном перемещении:

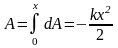
где – растяжение (удлинение) пружины.