1.Числовой ряд. Сходимость ряда. Необходимый признак сходимости ряда. Примеры.

Числовой ряд. Рассмотрим произвольную числовую последовательность и формально составим сумму ее членов Это выражение называют числовым рядом, или просто рядом. Члены последовательности называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда . Эта сумма называется n-ой частичной суммой.

Сходимость числового ряда. Ряд называют сходящимся, если существует и конечен предел последовательности частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают 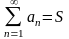. Если предел частичных сумм не существует или бесконечен, то ряд расходится.

Если ряд сходится, то предел общего члена равен 0 (необходимое условие сходимости ряда).

Док-во: Т.к. ряд сходится, то сущ пределы и . Т.к. суммы отличаются на слагаемое a_n=S_n-S_n-1, то

Пример

расходится

2. Признаки сравнения для рядов с положительными членами.

1. Рассмотрим два числовых ряда с неотрицательными членами . Тогда из сходимости ряда (2) следует сходимость ряда (1). Наоборот, из расходимости ряда (1) следует расходимость ряда (2).

2. Если для таких же двух рядов ,

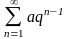существует конечный отличный от 0 предел отношений общих членов данных рядов то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд , который сходится при p>1 и расходится при p≤1, или геометрический ряд , который сходится при |q|≤1 и расходится при |q|≥1.

(Т.к. это геом прогрессия, то сумма S_n при |q|≠1

3,4. Признаки Даламбера и Коши.

Признак сходимости Даламбера. Пусть члены ряда неотрицательны. Если существует

то 1) при ρ<1 ряд сходится

2) при ρ>1 расходится

3) при ρ=1 нужны доп исследования

Док-во

1) пусть ρ<1, то существует q такое что ρ<q<1

Т.к. сущ , это означает что для любого ε>0 и в частности для ε=q-ρ найдется такой номер N, что для любого n>N будет спроаведливо нер-во

В частности

С некоторого номера n>N члены данного ряда меньше членов сход геом прогрессии

Следовательно на основании 1го признака сравнения, исслед ряд сходится.

2) пусть ρ>1. Это означает, что, начиная с некоторого номера будет спроаведливо нер-во

и т.к. каждый последующий член ряда больше предыдущего, то

. Необходимый признак сходимости не выполняется => ряд расходится

Радикальный признак сходимости Коши. Пусть

члены ряда

1) при ρ<1 ряд сходится

2) при ρ>1 расходится

3) при ρ=1 нужны доп исследования

Док-во

1)пусть ρ<1. Возьмем q удовл нер-ву ρ<q<1. Т.к. , то, начиная с некоторого номера будем иметь нер-во

Это нер-во показывает, что члены данного ряда, начиная с некоторого меньше соответствующих членов сходящейся геом прогрессии На основании 1 пр-ка сходимости данный ряд сход

2) пусть ρ>1. Это означает, что, начиная с некоторого номера, будет справедливо нер-во , т.е. не выполняется необходимое условие сходимости ряда, следовательно данный ряд расходится.

5.Интегральный признак Коши.

Пусть имеется ряд , члены которого монотонно не возрастают. Пусть имеется функция f(x), x в интервале [1,∞], монотонно не возрастающая и нерперывная на этом интервале, причем

Тогда для сходимости исходного ряда необходимо и достаточно, чтобы сходился интеграл

Замечание: функция может быть задана на промежутке [с,∞], тогда необходимо рассматривать интеграл .

Доказательство: рассмотрим ряд (2) Из свойств f(x) можно написать:

Интегрируя это неравенство на заданном промежутке, получим

Если (2) сходится, то из правой части неравенств по 1 признаку сравнения мы получаем, что исходный ряд сходится.

Если (2) расходится, то из левой части неравенств по 1 признаку сравнения мы получаем, что исходный ряд расходится.