2.7. Оценка устойчивости сау по частотному критерию

В качестве частотного критерия в курсовом проекте используется критерий устойчивости - годограф Михайлова (рис. 5). При использовании этого критерия в характеристическом уравнении замкнутой системы оператор р заменяется на оператор jω, а само уравнение преобразуется в комплексную формулу для построения годографа Михайлова:

, (24)

В уравнении (24) выделяются вещественная U и мнимая jV части:

;

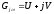Для построения на комплексной плоскости формула годографа с численными значениями входящих величин приводится к виду:

; (25)

Координаты точек графика вычисляются для значений частоты в пределах от нуля до бесконечности.

Если замкнутая САУ обладает частотной устойчивостью, то график годографа начинается на положительной части вещественной оси в точке с координатой U_ω=0, проходит последовательно в положительном направ­лении (против часовой стрелки) N квадрантов комплексной плоскости и устремляется в бесконечность (N - порядок уравнения).

Вычисленные координаты графика по формуле (25) для частот, рад/с,

ω=0;5;10;20;30;50;70;100...∞(табл.1) равны:

Таблица 1

ω	0	5	10	20	30	50	70	100	…	∞
U	440	439,83	439,32	437,28	433	423	406,68	372	…	-∞
V	0	0,738	1,404	2,232	1,908	-4,5	-22,428	-81	…	-∞

График годографа начинается на положительной части вещественной оси, проходит в направлении "против часовой стрелки", не охватывая начало координат и второй и третий квадрант.

Таким образом, оценка по частотному критерию показала, что исход­ная САУ не обладает устойчивостью.

2.8. Оценка запаса устойчивости по логарифмическим частотным характеристикам сау

В инженерных расчетах оценка запаса устойчивости систем автома­тического

управления производится с помощью логарифмических ампли­тудно-частотных (ЛАЧХ) и фазочастотных (ЛФЧХ) характеристик.

График ЛАЧХ представляет собой ломаную линию, каждый отрезок которой соответствует графику ЛАЧХ одного из элементов, составляющих структуру САУ.

График ЛФЧХ имеет вид непрерывной линии, кривизна которой зависит от параметров передаточных функций элементов системы.

При построении ЛАЧХ и ЛФЧХ по оси абсцисс откладывают значения частоты ω в логарифмическом масштабе. За единицу измерения частоты принята логарифмическая единица - декада, равная интервалу оси абсцисс, на котором частота изменяется в 10 раз.

На оси ординат при построении ЛАЧХ в равномерном масштабе откладывают логарифмическую амплитуду L(ω) передаточной функции, определяемую выражением:

, (26),

где W_jω–частотная передаточная функция разомкнутой системы.

За единицу измерения величины L(ω) принят децибел (дБ). Нуль логарифмической амплитуды в децибелах соответствует передаточному коэффициенту, численно равному единице, К^раз= 1.

При построении ЛФЧХ по оси ординат откладывают в равномерном масштабе угол сдвига фаз φ_ω в угловых градусах. ЛФЧХ строят непосредственно под графиком ЛАЧХ с одинаковыми масштабами абсцисс, для сопоставления фазового угла с изменением амплитуды при одинаковых частотах.

Наклон отрезков ломаной линии графика ЛАЧХ определяют в децибелах на декаду (дБ/дек.). Изломы графика ЛАЧХ имеют место при частотах, соответствующих постоянным времени типовых звеньев САУ и определяемых по формуле:

, (27)

где ω_i - частота сопряжения, 1/с; Т_i - постоянная времени, с.

Частота ω_с, при которой график ЛАЧХ пересекает ось абсцисс, называется частотой среза.

Для построения ЛАЧХ и ЛФЧХ используется зависимость для передаточной функции САУ в операторной форме по типу выражения (22).

;

Эта зависимость переводится в частотную форму путем замены оператора р на оператор jω:

; (28)

Логарифмируя (30) в соответствии с (28), получим формулу для построения ЛАХЧ в зависимости от частоты.

Подставляя известные значения получим:

Определим частоты сопряжения:

ω₁=1/0,08=12,5; ω₂=1/0,04=25; ω₃=1/0,03=33,3

Практическая формула для построения ЛАЧХ приобретает вид:

(29);

Строится ЛАЧХ график которой представляет собой ломаную линию, состоящую из трех участков, с переломами, соответствующими частотам сопряжения 12,5; 25; 33,3 1/с.

Горизонтальная линия графика (соответствующая первому члену уравнения

20 lgK^paз) проводится на высоте 52,8 дБ ординаты.

При значении абсциссы ω₁=12,5, линия графика, соответствующая инерционному звену, переламывается с наклоном -20 дБ/дек. и идет в направлении от точки А к точке В, где происходит следующий перелом.

При значении абсциссы ω₂=25 линия графика, соответствующая инер­ционному звену второго порядка, переламывается с наклоном -40 дБ/дек., по отношению к линии АВ и идет от точки В к токе С, где происходит следующий перелом.

При значении абсциссы ω₃=33,3 линия графика, соответствующая инер­ционному звену второго порядка, переламывается с наклоном -60 дБ/дек., по отношению к линии BC и идет от точки C в бесконечность.

Линия графика ЛАЧХ пересекает ось абсцисс в точке, соответствующей измеренной частоте среза ω_с= 127 1/с.

Для построения фазовой характеристики ЛФЧХ (в примере), на основе зависимости (31) составляется формула:

φ_ω = -arctg ω/12,5 – arctg ω/25- arctg ω/33,3 (30)

Подставляя в формулу (30) значения частоты (ω=0…∞), получим точки для построения ЛФЧХ:

φ₍₀₎ = 0

φ₍₁₎ = -6,29

φ_(12,5) = -65,58

φ₍₂₅₎ = -100,35

φ₍₃₃₎ = -114,45

φ₍₁₂₇₎ = -159,77

φ_(∞) = -270

На построенном графике ЛФЧХ пересечение линии графика с прямой линией на ординате -180 град, обозначено точкой М.

Запас устойчивости САУ количественно определяется двумя пара­метрами - запасом устойчивости по амплитуде h, дБ, и запасом устойчи­вости по фазе ∆φ, град.

Величина h измеряется на графике ЛАЧХ как ордината этого графика на частоте, соответствующей точке М на графике ЛФЧХ.

В нашем случае измеренный запас по амплитуде составляет h =35 дБ.

Величина ∆_φ измеряется как ордината графика ЛФЧХ, отсчитыва­емая от горизонтальной линии -180°, на частоте, соответствующей частоте среза ω_с на графике ЛАЧХ.

Измеренный запас по фазе составляет ∆_φ = -64,76°.

В курсовом проекте рекомендуется использовать следующие нормативные значения параметров запаса, соответствующие устойчивым системам:

-8дБ≥h≥ + 8дБ; ∆_φ ≥ + 24дБ. (31)

Анализ полученных в примере результатов показывает, что исходная САУ не обладает требуемым в соответствии с (31) запасом устойчивости по фазе, следовательно, система не может полностью обеспечивать рабочую функцию в соответствии с исходными данными на проекти­рование.

В инженерной практике используется способ повышения запаса устойчивости до требуемого уровня за счет дополнительного введения в структуру исходной САУ корректирующих звеньев.

С этой целью исходные частотные характеристики ЛАЧХ и ЛФЧХ графически преобразуются в желаемые характеристики - ЖЛАЧХ и ЖЛФЧХ, при которых САУ заведомо будет устойчивой.

На графике ЖЛАЧХ должен быть участок линии, пересека­ющий ось абсцисс с наклоном -20 дБ/дек на желаемой частоте среза ω_ж, отвечающей условию: ω_ж = (2,5...4) ω_с.

Принимаем: ω_ж =634 1/с.

Линия графика ЖЛАЧХ с наклоном - 20 дБ/дек проводится влево до пересечения с линией графика ЛАЧХ в точке D на частоте сопряжения ω₄ , а вправо - до точки E на частоте сопряжения ω₅. Частота сопряжения назначается по условию: ω₅ = (2...4) ω_ж. В примере получено: ω₄ = 96,4, ω₅=2536.

Построенный график ЖЛАЧХ представляет собой ломаную ли вершинами А, В, С, D, E и наклонами линий: АВ - 20 дБ/дек; ВС - 40 дБ/дек; CD - 60 дБ/дек; DE - 20 дБ/дек, далее от E — 60 дБ/дек.

Все переломы графика соответствуют инерционным звеньям. По известным частотам сопряжения и наклонам линий состав формула ЖЛАЧХ:

(32)

Выражение для ЖЛФЧХ составляется на основании формулы имеет вид:

φ_ω = -arctg ω/12,5 – arctg ω/25- arctg ω/33,3+2arctg ω/96,4- 2arctg ω/2536

Подставляя в формулу, получим значения:

φ₍₀₎ = 0

φ₍₁₎ = -8,26

φ_(12,5) = -78

φ₍₂₅₎ = -118

φ_(33,3) = -130,91

φ_(96,4) = -143

φ₍₁₀₀₎ = -142,84

φ₍₆₃₄₎ = -129

φ₍₁₀₀₀₎ = -140

φ₍₂₅₃₆₎ = -183

φ_(∞) = -270

На графиках ЖЛАЧХ и ЖЛФЧХ обозначаются ординаты h и ∆φ, определяющие запасы устойчивости. В примере эти измеренные величины составили: h = -7 дБ, ∆φ = 51 . Сравнение этих величин с нормативными значениями (32) показывает, что полученные желаемые частотные характеристики соответствуют САУ, обладающей запасом устойчивости как по амплитуде, так и по фазе.

Для получения математической зависимости L_(w)кор, определяющей параметры вводимых корректирующих звеньев, производится алгебраическое сложение зависимостей для ЖЛАЧХ и ЛАЧХ:

L_(w)кор= L_(w)ж -L_(w) (33)

Используя формулы (29) и (32), из (33) получим:

Упрощая, получим: (34)

Частотная передаточная функция корректирующего устройства составляется обратным преобразованием из формулы (34):

,

где Т_К1,Т_К2 - постоянные времени корректирующих звеньев инерцион­ного вида. В примере эти величины имеют численные значения:

Т_К1=1/w₄=0,004, Т_К2=1/w₅= 0,001

Подставляя численные значения из примера получим передаточную функцию:

(34)

Частотная передаточная функция разомкнутой САУ, откорректи­рованная введением дополнительных звеньев (34), примет вид:

Передаточная функция в операторной форме для откорректи­рованной разомкнутой САУ будет иметь вид: