
Физика аэрозолей / Физ.аэрозолей 1
.docxМинистерство
образования и науки Российской Федерации

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра экспериментальной физики атмосферы
Дисциплина «Экспериментальная физика аэрозолей»
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
Исследование функции распределения аэрозолей по размерам
Вариант №2
Выполнили:
ст. гр. ПМ-Б15-1-3 ___________________ Светачева А. Скачков И.
Проверил:
доц. каф. ЭФА ___________________ Чукин В.В.
Санкт-Петербург 2017
Цель работы:
Определить полную концентрацию аэрозолей по результатам измерения прибором
DSM-501.
Теоретические сведения:
Аэрозоли в атмосфере имеют различные размеры. Для того чтобы описать содержание
аэрозолей используют функцию распределения аэрозолей по размерам. Часто для этой
цели используется так называемое гамма- распределение:
![]()
где a, b, c – параметры распределения.
Главным свойством этой функции является то, что интеграл от нее по всему диапазону
размеров
частиц дает значение полной концентрации
аэрозолей:

Часто приборы, измеряющие содержание аэрозолей, получают значения содержания
аэрозолей менее определенного размера (на входе приборов используются импакторы,
захватывающие
крупные частицы):
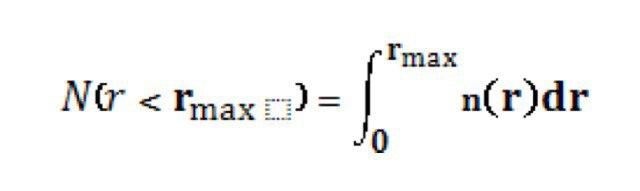
или более заданного размера (например, фотодетектор не реагирует на слабые
отраженные
сигналы ниже заданного порога):

Параметры распределения могут быть выражены через модальный, средний и
эффективный
радиусы:
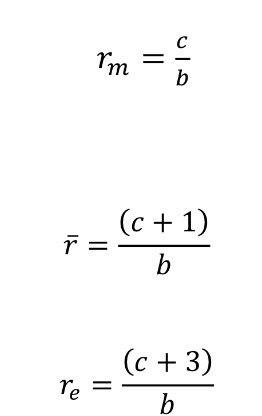
Порядок выполнения работы:
Для определения параметров распределения аэрозолей по размерам по заданном
модальном
радиусе найдены формулы:
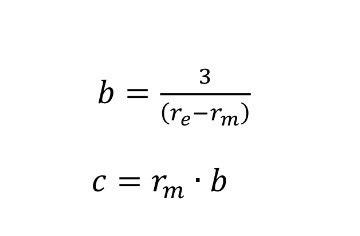
r =3*10^-8 м и эффективном радиусе r = 2.9 *10^-7 м аэрозолей
Затем, составлена программа на языке программирования Python, которая
позволила рассчитать функцию распределения аэрозолей по размерам,
представленную на рисунке 1.

Текст скрипта:
#!/usr/bin/env python
# coding: utf8
from numpy import *
from math import *
from matplotlib.pyplot import *
#################################################################################
# Дисциплина:
# ЭКСПЕРИМЕНТАЛЬНАЯ ФИЗИКА АЭРОЗОЛЕЙ
# Пример 1A:
# ИНТЕГРИРОВАНИЕ ФУНКЦИИ РАСПЕРЕДЕЛЕНИЯ АЭРОЗОЛЕЙ ПО РАЗМЕРАМ
# Авторы:
# Чукин Владимир Владимирович <chukin@meteolab.ru>
# Чукина Александра Михайловна <chukina@meteolab.ru>
# Садыкова Алися Фаилевна <sadykova@meteolab.ru>
# Воробъёва Ольга Владимировна <vorobyeva@meteolab.ru>
# Версия:
# 2016-09-19
#################################################################################
#################################################################################
# Задаем параметры распередения аэрозолей по размерам
#################################################################################
N1= 50.0 # Концентрация аэрозолей, м-3
rmean = 1.21E-7 # Средний радиус аэрозолей, м
reff = 2.9E-7 # Эффективный радиус аэрозолей, м
rmod =3.0E-8 # Модальный радиус аэрозолей, м
b =3.0 /(reff - rmod) # Коэффициент "b"гамма-распределения
c = rmod * b # Коэффициент "c"гамма-распределения
a = 1.0 * b**(c+1.0) / gamma(c+1.0) # Коэффициент "a"гамма-распределения
#################################################################################
# Создаем вспомогательные массивы
#################################################################################
rmin = 1.0E-6 # Начальный радиус интегрирования
rmax = 1.0E-3 # Конечный радиус интегрирования
p = linspace(log10(rmin),log10(rmax),1000) # Массив степеней радиусов аэрозолей
r = 10**p # Массив радиусов аэрозолей
n = zeros(len(r)) # Массив функции распределения
#################################################################################
# Способ №1 (универсальный)
# Определяем концентрацию аэрозолей как интеграл от функции
# распределения аэрозолей по размерам
#################################################################################
summa = 0.0 # Начальное значение суммы
for i in range(1, len(r)-1): # Перебираем в цикле значения радиусов n[i] = a*r[i]**c * exp(-
b*r[i]) # Функция распределения по размерам dr = 0.5*(r[i+1]-r[i-1]) # Шаг
интегрирования,м
summa = summa + n[i]*dr # Интеграл от распределения по размерам
N = N1/summa
#################################################################################
# Способ №2 (быстрый)
# Определяем полную концентрацию аэрозолей по параметрам гамма-распределения
#################################################################################
#################################################################################
# Печать параметров распределения аэрозолей по размерам
#################################################################################
print "a =", a print "b =", b print
"c =", c
print "Rmod =", rmod print "Rmean =",
rmean print "Reff =", reff
print "N =", N
#################################################################################
# Построение графика
#################################################################################
semilogx(r, n, color="red") xlabel("r, m")
ylabel("n(r), m-4") grid(True)
show()
Результаты, выданные программой:
*** Remote Interpreter Reinitialized ***
>>>
a = 3602402926.13
b = 11538461.5385
c = 0.346153846154
Rmod = 3e-08 Rmean = 1.21e-
07 Reff = 2.9e-07
N = 1982921.14075
>>>
Для графика:
При rmin = 1.0E-9
*** Remote Interpreter Reinitialized ***
>>>
a = 3602402926.13
b = 11538461.5385
c = 0.346153846154
Rmod = 3e-08
Rmean = 1.21e-07
Reff = 2.9e-07
N = 50.10147022
Анализ полученных результатов:
В результате определения параметров распределения аэрозолей по размерам и
численного интегрирования этой функции определено значение полной концентрации
аэрозолей, которое составило 1.9·10^+6м^-3. Это значение оказалось выше, чем
результаты измерения прибором DSM-501, составившие 5.0·10^1 м^-3. Это связано с
чувствительностью данного прибора только к грубодисперсным аэрозолям, которых
крайне мало в атмосфере.
Выводы по работе:
По данным измерений содержания грубодисперсной части аэрозолей возможно
восстановление полной концентрации аэрозолей в воздухе с использованием
априорной информации о распределении аэрозолей по размерам в виде гамма-
функции.
