1. Матрицы: определение, виды.

Матрицей называется прямоугольная таблица чисел, содержащая m-строк и n-столбцов.

Виды матриц:

- Верхняя треугольная матрица;

- Диагональная матрица;

- Единичная матрица;

- Нулевая матрица.

2. Действия с матрицами: транспонирование, сложение, умножение на число, умножение матриц.

- Матрица, полученная из данной путем замены каждой ее строчки столбцом с тем же номером, называется матрицей транспонированной к данной (А^Т);

- Сумма двух матриц А и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В;

- Произведение матрицы А на число лямбда λ (не = 0) называется матрица, полученная из матрицы А путем умножения всех ее элементов на число лямбда λ;

- Произведение матриц А и В равно матрице С, когда соответствующая строка первой матрицы умножается на соответствующий столбец второй матрицы и только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы.

3. Элементарные преобразования матриц. Правило прямоугольника.

Элементарные преобразования:

- Перестановка строк или столбцов;

- Умножение строки или столбца на число, отличное от 0;

- Прибавление к элементам строки или столбца соответствующих элементов другой строки или столбца, предварительно умноженных на некоторое число;

- Транспонирование;

- Вычеркивание нулевой строки или столбца или вычеркивание одной из двух одинаковых строк или столбцов.

Правило прямоугольника:

- на каждом шаге выбираем разрешающий элемент; строку и столбец, содержащие разрешающий элемент будем называть разрешающим;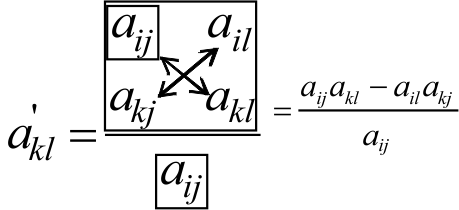

-элементы разрешающей строки переписываем без изменений, элементы разрешающего столбца заменяем нулями, все другие элементы вычисляются по правилу:

4. Ранг матрицы. Свойства ранга матрицы.

Рангом матрицы А (обозначение: R(А) или r(А)) называется наивысший порядок минора матрицы, отличный от нуля.

Свойства:

- ранг матрицы выражается целым числом между 0 и меньшим из чисел n, m;

- при транспонировании ранг матрицы не меняется;

- ранг матрицы равен нулю, если матрица является нулевой;

- если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится;

- для квадратной матрицы n-ого порядка r=n если матрица невырожденная.

5. Правило Саррюса, правило треугольника, метод Крамера для вычисления определителей третьего порядка. Теорема о свойствах определителей.

Правило Саррюса. Для вычисления определителя третьего порядка, допишем два первых столбца и перемножим диагональные элементы, взяв произведение со знаком «плюс», если диагональ является главной или параллельна её и, взяв произведение со знаком «минус», если диагональ является побочной или параллельной ей: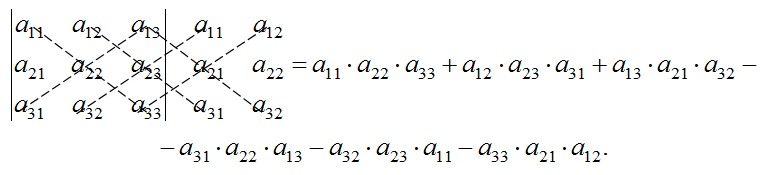

Правило треугольника. Определителем матрицы третьего порядка можно вычислить по формуле или схеме: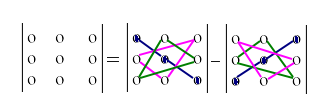

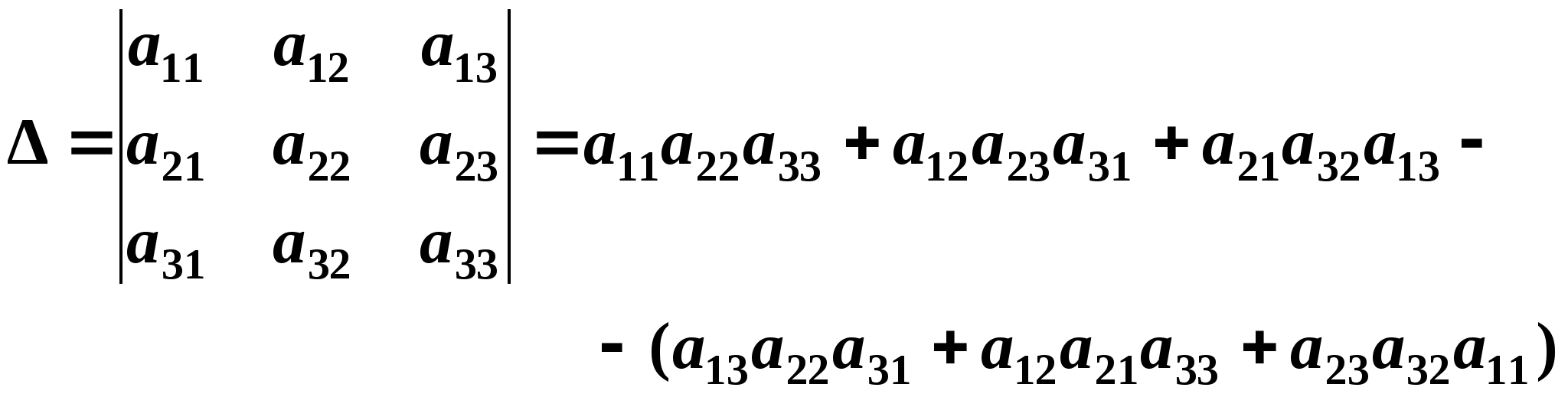
Метод Крамера. Вычисляем определитель основной матрицы системы и убеждаемся, что он отличен от нуля; находим определители, которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов; вычисляем искомые неизвестные переменные x₁, x₂, …, x_n по формулам: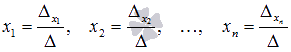

6. Миноры и алгебраические дополнения.

Минором Mij элемента aij матрицы An×n именуют определитель матрицы, полученной из матрицы A вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент aij).

Алгебраическое дополнением Aij элемента aij матрицы An×n находится по следующей формуле: Aij=(−1)i+j⋅Mij, где Mij – минор элемента aij.

7. Теорема о разложении определителя по строке (столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения.

Иначе говоря, имеет место разложение d по элементам i-й строки: d = a_{i 1} A_{i 1} + a_{i 2} A_{i 2} +... + a_{i n} A_{i n} (i = ) или j- го столбца: d = a_{1 j} A_{1 j} + a_{2 j} A_{2 j} +... + a_n j A_n j (j = ).

8. Обратная матрица. Теорема о нахождении обратной матрицы через союзную.

Матрица называется обратной по отношению к квадратной матрице А если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е. А^-1 * А = А * А^-1 = Е.

Формула нахождения:

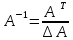
Теорема нахождения через союзную матрицу:

- вычислить определитель матрицы А, если ΔА не равен 0, то обратная матрица существует;

- найти союзную матрицу А^~, элементами которой являются алгебраические дополнения элементов исходной матрицы;

- найти обратную матрицу по формуле.

9. Системы линейных алгебраических уравнений (СЛАУ). Основная и расширенная матрицы СЛАУ.

Система линейных алгебраических уравнений — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.

Основная матрица – матрица, состоящая из коэффициентов при неизвестных.

Расширенная матрица – матрица, полученная путем добавления справа от основной матрицы столбца свободных членов.

10. Совместные СЛАУ. Теорема Кронекера-Капелли.

СЛАУ является совместной, если она имеет хотя бы одно решение.

Теорема Кронекера-Капелли: СЛАУ совместна тогда и только тогда, когда ранг её основной матрицы A равен рангу её расширенной матрицы Ā, т.е. r(A) = r(Ā)

11. Решение систем линейных алгебраических уравнений: матричный метод.

Решение СЛАУ матричным методом определяется по формуле X = A^-1 * B, где A^-1 – обратная матрица, В – матрица свободных членов уравнения.

Метод решения:

-находим определитель матрицы А;

-находим обратную матрицу А^-1  при помощи союзной матрицы. Вычисляем алгебраические дополнения Аij к соответствующим элементам матрицы А;

-умножаем обратную матрицу А^-1 на столбец свободных членов В и получаем решение системы.

12. Решение систем линейных алгебраических уравнений: метод Гаусса.

Метод Гаусса состоит в преобразовании расширенной матрицы системы к диагональному виду, с точностью до перестановки строк или столбцов, что позволяет сразу получить решение системы.

Метод решения:

-записать расширенную матрицу;

-выполнять элементарные преобразования до тех пор, пока матрица не перейдет к диагональному виду.

13. Решение систем линейных уравнений по формулам Крамера.

Любая крамеровская система уравнений имеет единственное решение, которое определяется формулой: 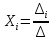, где 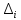– определитель матрицы, полученной из основной матрицы A заменой i-го столбца на столбец свободных членов системы, а  – определитель основной матрицы. Эта формула называется формулой Крамера.