§1.4. Биномиальное распределение молекул в объеме.

Пусть N молекул находятся в объеме V. Выделим объем V₁ в объеме V. Будем интересоваться макросостоянием, когда в объеме V₁ находится n частиц, а в оставшемся объеме (V - V₁) находится (N - n) молекул. Вероятность того, что одна молекула находится в V₁, равна V₁/V. Вероятность, что две частицы находятся в объеме V₁, равна 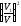. Вероятность того, что n частиц в V₁: - . Остальные (N - n) молекул должны быть в оставшемся объеме (V - V₁), т.е. нужно учесть вероятность того, что они попали в этот объем, которая равна

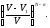Итак, полная вероятность такого “микросостояния”

(1.19)

Введем понятие статистического веса (), т.е. числа способов, которым реализуется данное макросостояние из различных микросостояний. Так как макросостояние газа не зависит от перестановок частиц, то

(1.20)

Итак, полная вероятность данного макросостояния равна

(1.21)

Введем обозначения

, . (1.22)

Полученное распределение вероятностей

(1.23)

называется биномиальным распределением. Название произошло от сходства с алгебраическим биномом Ньютона:

Свойства биномиального распределения:

1) По определению, p + q = 1,

2) Ясно, что вероятность состояния с очень малыми n или (N - n) при фиксированных V₁ и V очень мала, так как при этом 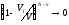или , или .

В общем случае нас интересуют достаточно большие N и n, когда переход от вероятности к вероятности осуществляется непрерывным образом. Иначе говоря, мы полагаем, что dn = 1 мала по сравнению с N. Возьмем теперь разность вероятностей двух соседних состояний и приравняем ее нулю, чтобы найти максимум вероятности:

(1.24)

Из равенства нулю выражения в скобках имеем: _, .

Так как N >> 1 и n >> 1, получаем

. (1.25)

Поскольку - концентрация молекул в объеме, то наиболее вероятное состояние осуществляется тогда, когда число молекул в объеме V₁ равно

n = n₀V₁, т.е. когда осуществляется равномерное распределение молекул по всему объему. Такое состояние называется стационарным или равновесным.

Определение: равновесным состоянием системы является ее наиболее вероятное состояние.

Схематически картина распределения вероятности при достаточно больших значениях числах частиц N и n выглядит как показано на рисунке (дискретные точки соединены сплошной линией) в виде острого максимума в окрестности n_вер c очень маленькой шириной n. Условие нормировки может быть записано

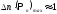
Если за газом наблюдать достаточно большое время, то окажется, что более вероятные распределения молекул возникают чаще, чем менее вероятные. Поэтому с течением времени газ именно и переходит в наиболее вероятные состояния, причем, достигнув наиболее вероятного состояния, газ в нем практически и остается. Существенно, что равновесное состояние газа не зависит от предыстории (или начального состояния), т.е. от “пути”, которым газ шел к равновесию. Независимость от предыстории и постоянство во времени свойств газа в равновесии имеют своим следствием то, что равновесный газ можно описать небольшим числом макроскопических величин, характеризующих газ в целом (для идеального газа - P, V, T).

Итак, вероятность того, что число частиц в объеме V₁ отклонится даже незначительно от n_max, ничтожна и быстро убывает с величиной отклонения. Но, тем не менее, число молекул в V₁ не всегда строго равно n_max , а колеблется (флуктуирует) около этой величины.

Флуктуации числа молекул в объеме.

Ранее мы ввели дисперсию и относительную квадратичную флуктуацию 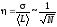, где N - число испытаний (число молекул). Рассмотрим флуктуации для биномиального распределения.

Среднее значение числа молекул в объеме V₁ равно

(1.26)

Чтобы сосчитать данную сумму, воспользуемся красивым формальным приемом. Запишем среднее значение через производную:

(1.27)

На самом деле p + q = 1, но такое значение подставлять сразу нельзя. Этим можно воспользоваться только после вычисления производной.

(1.28)

Интересно отметить, что среднее значение совпадает с наиболее вероятным значением n, т.е. соответствует равномерному заполнению всего сосуда. Когда V₁ = V/2, получаем .

Относительная квадратичная флуктуация.

Чтобы сосчитать квадратичную флуктуацию (дисперсию) необходимо знать . Вычислим аналогично тому, как это делалось в предыдущем пункте:

Здесь мы воспользовались тем, что p + q = 1. Итак,

. (1.29)

Сосчитаем теперь относительную квадратичную флуктуацию. Сначала запишем дисперсию, которая равна

, (1.30)

и тогда для относительной квадратичной флуктуации получаем

. (1.31)

Важно, что относительная квадратичная флуктуация убывает с ростом числа частиц в системе . Физическое содержание полученного выражения очень важно. Исследуем его. Подставим в относительную квадратичную флуктуацию выражения для p и q из (1.22):

(1.32)

Рассмотрим большой объем V₁  V, тогда относительная флуктуация стремится к нулю (  0), т.к. число частиц в объеме V фиксировано.

При уменьшении объема V₁ (V₁  0) относительная флуктуация возрастает, т.е. при V₁ << V имеем

Для частиц в рассматриваемом объеме V₁ = V/2 относительная флуктуация равна .

Для газа, находящегося в нормальных условиях, частиц/мм³. При V₁ << V получаем очень малую величину относительной квадратичной флуктуации

Итак, в макроскопических системах статистические флуктуации незначительны. С большой точностью все величины равны своим средним значениям. Иначе говоря, подавляющую часть времени газ находится в состояниях, в которых отклонения числа молекул от среднего не превышают относительную флуктуацию.