
- •60 Вопросов 60 ответов
- •1. Алгоритм работы системы управления с отрицательной обратной связью.
- •2. Функциональная схема. Основные элементы систем управления
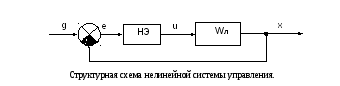
- •3. Структурная схема системы управления. Сигналы, действующие в системах
- •4. Входы, выходы систем управления
- •5. Назначение систем управления
- •6. Функциональный, структурный анализ системы управления
- •7. Примеры систем управления
- •8. Классификация систем управления
- •Разомкнутая система управления по возмущающему воздействию
- •Замкнутая система или система с оос.
- •Комбинированная система.
- •9. Типовые модели детерминированных сигналов
- •1. Модели детерминированных сигналов.
- •Линейное и квадратичное воздействие и
- •10. Характеристики случайных сигналов
- •Решение дифференциального уравнения 1-го порядка классическим методом
- •17. Решение дифференциального уравнения численным методом Эйлера
- •18. Операторный метод решения дифференциальных уравнений.
- •20. Получение передаточных функций из дифференциальных уравнений.
- •Методы прямого, обратного преобразования Лапласа (таблицы, MathCad).
- •22. Линеаризация статических и динамических характеристик.
- •23. Статические и динамические характеристики элементов (системы)
- •24. Статическая характеристика. Статические, астатические элементы.
- •25. Временные характеристики динамических звеньев
- •26. Частотные характеристики динамических звеньев
- •27. Логарифмические частотные характеристики.
- •28. Дифференциальное уравнение n-го порядка. Модели основных типовых звеньев.
- •29. Усилительное звено. Математическая модель, характеристики.
- •30. Апериодическое звено первого порядка. Математическая модель, характеристики.
- •31. Интегрирующее звено. Математическая модель, характеристики.
- •32. Дифференцирующее звено. Математическая модель, характеристики.
- •33. Звено второго порядка. Математическая модель, характеристики.
- •34. Эквивалентные модели последовательного, параллельного, встречно-параллельного соединений элементов системы управления.
- •18. Виды передаточных функций системы управления, их определение по передаточным функциям элементов системы.
- •Показатели качества переходных процессов. Точность установившегося режима.
- •19. Методы разработки систем управления.
- •Пид регулятор, его составляющие
- •Назначение дифференциальной составляющей регулятора.
- •Амплитудная фазовая частотная характеристика системы с п-, пи-, пид – регулятором. Вопрос рассмотрен выше в пунктах 28-30.
- •Разработка системы управления заданной структуры методом мм.
- •Методика моделирования линейной системы с пид регулятором в системе Simulink.
- •Получение в Simulink для системы с пид регулятором
- •Устранение в системе с пид регулятором статической ошибки.
- •Методика настройки пид регулятора.
- •Введение в нелинейные системы управления. Существенные отличия от линейных.
- •Математическая модель нелинейного элемента насыщения.
- •Математическая модель нелинейного элемента с зоной нечувствительности.
- •Методика анализа нелинейной сау методом математического моделирования.
- •Преобразование моделей непрерывных систем к уравнению Коши.
- •Классический метод решения дифференциальных уравнений:
- •1. Упрощение временных функций.
- •3) Обратное преобразование Лапласа.
-
Математическая модель нелинейного элемента насыщения.

-
Математическая модель нелинейного элемента с зоной нечувствительности.

-
Методика анализа нелинейной сау методом математического моделирования.
Разработка системы управления с заданной структурой в системе Simulink позволяет исследовать работоспособность системы, определить устойчивость системы, качественные показатели работы системы при изменении задающего воздействия, при отработке возмущающих воздействий, определить параметры системы, обеспечивающие работу системы с качественными показателями.
Порядок подготовки исходных данных и проведения моделирования системы.
1. Для элементов системы управления: задающего устройства, элемента сравнения, релейного элемента, усилителя, исполнительного механизма, объекта управления, датчика регулируемой величины построить математические модели. Путем структурных преобразований линейные элементы привести к одному элементу, и систему привести к типовому виду систем с нелинейным элементом.

-
Подготовить в системе Simulink математическую модель для моделирования системы управления, приведенную на рисунке. Ввести данные для элементов.

-
В
 текстовом редакторе ввести оператор
функцию для релейного элемента.
Например, для релейного элемента,
приведенного на рисунке она имеет вид:
текстовом редакторе ввести оператор
функцию для релейного элемента.
Например, для релейного элемента,
приведенного на рисунке она имеет вид:


-
Провести моделирование системы. Выбрать длительность интервала моделирования, обеспечивающую наглядность анализа работы системы.
-
Исследовать и построить графики переходных процессов при отработке системой заданного и возмущающего воздействий.
-
Исследовать влияние зоны нечувствительности на ошибку регулирования, автоколебания в системе, продолжительность переходного процесса.
-
Исследовать влияние величины сигнала на выходе релейного элемента.
-
Исследовать влияние постоянных времени элементов линейной части системы.
-
Исследовать возможность образования и параметры автоколебательных режимов в
-
системе управления.
-
Сделать выводы по работоспособности системы и необходимости ее доработки.
46-47, 49-50. Метод фазовой плоскости и его применение. Анализ САУ на фазовой плоскости. Анализ фазовых траекторий методом припасовывания (путем численного решения дифференциальных уравнений). Построение фазовых траекторий, переходных процессов в MathCad.
На фазовой плоскости удобно исследовать нелинейные системы управления второго порядка. При этом по оси абсцисс откладывается выходная переменная системы управления, которая, согласно структурной схеме, является и входной переменной нелинейного элемента. По оси ординат удобно откладывать производную выходной переменной.
В ТАУ есть специальный метод построения фазовых траекторий. Но на компьютере удобно строить фазовые траектории путем численного интегрирования системы уравнений, описывающих работу системы управления. При численном интегрировании на каждом шаге расчета производится анализ состояния нелинейного элемента, и линейная часть рассчитывается для конкретного состояния входного сигнала. При этом следующие друг за другом результаты расчета являются продолжением предыдущих результатов, т.е. последующие решения припасовываются к предыдущим. Отсюда название метода – метод припасовывания.
Порядок исследования нелинейной системы на фазовой плоскости.
-
Строится математическая модель линейной части системы и записывается в форме Коши.
Например, передаточная функция второго порядка линейной части имеет вид:
![]() Дифференциальное уравнение будет
Дифференциальное уравнение будет
![]()
С учетом нелинейной функции нелинейного
элемента
![]() и
отрицательного знака для величины х
на элементе сравнения уравнение будет
иметь вид
и
отрицательного знака для величины х
на элементе сравнения уравнение будет
иметь вид
![]()
Перепишем уравнение, оставив в левой части только старшую производную,
![]() введем переменную
введем переменную
![]() и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши

-
Построим математическую модель нелинейного элемента. Пусть используется реле с зоной нечувствительности b без гистерезиса. Нелинейность опишем в виде логической функции.


В зависимости от значения x
имеем три зоны, в которых правая часть
системы уравнений Коши будет иметь
различный вид. Запишем систему уравнений
в виде трех пар уравнений, значение F(x)
в которых определяется логикой работы
реле. В первых двух системах уравнения
изменяется знак при управляющем
воздействии u, в
последней управляющее воздействие
![]()

Система управления описана системой
дифференциальных уравнений. Теперь
можно задать количественные значения
параметров, начальные условия по
координатам
![]() и, используя алгоритм численного
интегрирования системы дифференциальных
уравнений, найти движение системы.
и, используя алгоритм численного
интегрирования системы дифференциальных
уравнений, найти движение системы.
Пусть
![]()
![]()
![]()
![]()
Зададимся начальными значениями
![]()
![]()
-
Используя метод Рунге-Кутта с фиксированным шагом, найдем решение системы
![]()
здесь: x01 – вектор начальных условий,
0-100 – отрезок времени, на котором ищется решение.
1000 – количество точек решения на заданном отрезке времени.
DU - система дифференциальных уравнений.
Решением является матрица X1, имеющая 3 столбца (1-й столбец время, второй, третий столбцы вектор искомых переменных – выходная переменная и ее производная) и 1000 строк по количеству ординат решения системы уравнений.
Необходимо помнить, что нумерация столбцов и строк по умолчанию в MathCad начинается с 0.
График движения фазовой точки на фазовой плоскости имеет вид
Здесь: по оси абсцисс второй столбец вектора Х1, по оси ординат третий столбец X1.

-
Построение графика переходного процесса.

Здесь: по оси абсцисс - время (первый столбец вектора Х1), по оси ординат - выходная координата системы (второй столбец X1).
-
Анализ результатов моделирования.
Система управления устойчивая, не имеет автоколебательного режима.
Ошибка несколько раз изменяет знак, скорость также бывает положительной –система разгоняется и отрицательной – система тормозится.
Остаточная ошибка системы находится в пределах зоны нечувствительности реле.
Время регулирования составляет около
50 сек (дискретов
![]() по времени).
по времени).
