- •Вопрос 2.
- •Часть 1.Количественная мера информации для равновозможных событий
- •Часть 2. Мера р. Хартли
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6. Свойства энтропии источника дискретных сообщений
- •Вопрос 7. Энтропия источника совместных сообщений
- •Вопрос 8. Что такое условная энтропия?
- •Вопрос 9.
- •Вопрос 10. Свойства количественной меры информации при неполной достоверности результатов опыта.
- •Вопрос 11. Вычисление количественной меры информации для двоичного канала с помехами.
- •Вопрос 12. Как оценивается избыточность источника сообщений?
- •Вопрос 13.
- •Вопрос 23.
- •Вопрос 24. Приведите модель двоичного канала с шумами
- •Вопрос 25.
- •Вопрос26. Формула Шеннона для аналогового канала с шумами.
- •Вопрос 27. Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •Вопрос 28. Принципы помехоустойчивого кодирования. Кодовое расстояние.
- •Вопрос 29. Вероятность ошибочного приема кодовой информации для простого двоичного кода и для кода с исправлением ошибок кратности t.
- •Вопрос 30. Простейшие избыточные коды.
- •Вопрос 31. Групповой код Хемминга. Принципы построения. Синдром ошибки. Коды с обнаружением и исправлением ошибок. Код хемминга
- •Вопрос 32. Определение числа проверочных элементов.
- •Вопрос 33. Определение проверочных элементов, входящих в каждую группу. Исправляющая способность кода хемминга
Вопрос 7. Энтропия источника совместных сообщений
Возьмем
два ансамбля событий:
 ,
который представляется (1.4)
,
который представляется (1.4)
 ,
и
,
и
 ,
описываемый как
,
описываемый как
 .
(1.11)
.
(1.11)
Будем
рассматривать совместные (происходящие
вместе) события
 и
и
 .
Все возможные пары
.
Все возможные пары
 могут рассматриваться как элементы
нового объединенного ансамбля
могут рассматриваться как элементы
нового объединенного ансамбля
 .
В качестве примера совместных событий
.
В качестве примера совместных событий
 и
и
 можно отметить состояния
можно отметить состояния
 и
и
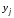 ,
формируемые в r-
и s-разрядных
регистрах, широко используемых в
информационных системах. При этом число
состояний r-разрядного
регистра составит
,
формируемые в r-
и s-разрядных
регистрах, широко используемых в
информационных системах. При этом число
состояний r-разрядного
регистра составит
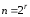 ,
а s-разрядного
–
,
а s-разрядного
–
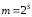 .
Каждому из состояний регистров с помощью
логических дешифраторов можно привести
в соответствие двоичные сигналы (события)
.
Каждому из состояний регистров с помощью
логических дешифраторов можно привести
в соответствие двоичные сигналы (события)
 (
( )
и
)
и
 (
( ).
Все возможные пары
).
Все возможные пары
 и
и
 могут быть реализованы с использованием
двухвходовых логических элементов «И»
(конъюнкторов). Таким образом, на выходах
этих логических элементов получим
могут быть реализованы с использованием
двухвходовых логических элементов «И»
(конъюнкторов). Таким образом, на выходах
этих логических элементов получим
 двоичных сигналов (сообщений), которые
можно рассматривать как элементы нового
ансамбля
двоичных сигналов (сообщений), которые
можно рассматривать как элементы нового
ансамбля
 .
.
Объединенный ансамбль таких сообщений представим в виде
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
… |
|
Ансамбль
 может рассматриваться как некий новый,
в котором возможны
может рассматриваться как некий новый,
в котором возможны
 различных состояний (событий)
различных состояний (событий)
 с заданным распределением вероятностей
с заданным распределением вероятностей
 .
.
Энтропия
такого ансамбля, т.е. энтропия исхода
совместных событий
 ,
может быть получена по аналогии с
энтропией
,
может быть получена по аналогии с
энтропией
 (1.8) в следующем виде:
(1.8) в следующем виде:
 .
(1.12)
.
(1.12)
Известно, что вероятность совместного события равна произведению вероятности одного события на условную вероятность другого события, при условии, что произошло первое событие [3]
 ,
(1.13)
,
(1.13)
где
 – вероятность события
– вероятность события
 при условии, что произошло событие
при условии, что произошло событие
 (условная вероятность
(условная вероятность
 ),
),
 – условная вероятность
– условная вероятность
 .
.
Проделав подстановку (1.13) в (1.12) и соответствующие преобразования, получим
 .
(1.14)
.
(1.14)
Вопрос 8. Что такое условная энтропия?
Для
условных вероятностей известно, что
 [3],
тогда выражение (1.14) с учетом (1.8) можно
привести к виду
[3],
тогда выражение (1.14) с учетом (1.8) можно
привести к виду
 ,
(1.15)
,
(1.15)
где
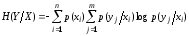 .
(1.16)
.
(1.16)
Здесь
 будем называть условной энтропией
ансамбля
будем называть условной энтропией
ансамбля
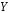 .
Условную энтропию структурно можно
рассматривать как математическое
ожидание частных условных энтропий
.
Условную энтропию структурно можно
рассматривать как математическое
ожидание частных условных энтропий
 ансамбля
ансамбля
 .
Следовательно, условная энтропия
.
Следовательно, условная энтропия
 равна среднему значению частных условных
энтропий и характеризует неопределенность
исхода событий
равна среднему значению частных условных
энтропий и характеризует неопределенность
исхода событий
 при известных событиях
при известных событиях
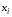 :
:
 .
.
Легко
видеть, что условная энтропия
 ,
так же как энтропии
,
так же как энтропии
 и
и
 ,
– величина положительная, т.е.
,
– величина положительная, т.е.
 .
.
Обратим внимание на то, что формула (1.13) для вероятности совместных событий, по сути, имеет две формы записи. Используя это, нетрудно представить и энтропию совместных событий в двух видах:
 .
(1.17)
.
(1.17)
Вопрос 9.
Определение количества информации источника дискретных сообщений при неполной достоверности результатов опыта
Как уже отмечалось, информация о том или ином событии или факте добывается всегда в результате целенаправленного опыта, причем после опыта ситуация оказывается не всегда полностью определенной, и мы не можем с полной достоверностью утверждать, какое именно событие имело место. Требуется определить количество информации, приходящееся в среднем на один опыт, когда полная достоверность его исхода отсутствует.
Пусть
интересующие нас события или факты
составляют ансамбль
 (1.4) (переданные сообщения)
(1.4) (переданные сообщения)
 ,
,
а
результаты опыта, на основе которых мы
выносим суждение об исходе событий
 ,
составляют ансамбль
,
составляют ансамбль
 (1.11) (принятые сообщения)
(1.11) (принятые сообщения)
 .
.
Обозначим
через
 вероятность того, что при известном
исходе опыта
вероятность того, что при известном
исходе опыта
 имело место событие
имело место событие
 .
Если, например,
.
Если, например,
 (1.18)
(1.18)
то
в результате опыта ситуация полностью
определена, и мы можем с полной
достоверностью утверждать, какое событие
(сообщение)
 имело место. Так как неопределенность
исхода событий
имело место. Так как неопределенность
исхода событий
 до опыта равна
до опыта равна
 ,
а после опыта неопределенность
отсутствует, то в этом случае
,
а после опыта неопределенность
отсутствует, то в этом случае
 (1.19)
(1.19)
где
 – количество информации, содержащееся
в среднем в опытах
– количество информации, содержащееся
в среднем в опытах
 относительно интересующих нас событий
относительно интересующих нас событий
 .
.
В
более общем случае, когда
 для различных
для различных
 ,
после опыта сохранится неопределенность,
которая, очевидно, приведет к уменьшению
количества информации (1.19).
,
после опыта сохранится неопределенность,
которая, очевидно, приведет к уменьшению
количества информации (1.19).
Количество
информации, содержащееся в опыте
 относительно событий
относительно событий
 ,
которое назовем частной мерой количества
информации при ее неполной достоверности,
можно определить по формуле (1.2) как
,
которое назовем частной мерой количества
информации при ее неполной достоверности,
можно определить по формуле (1.2) как
 .
(1.20)
.
(1.20)
Здесь
условная вероятность
 определяет послеопытную вероятность
определяет послеопытную вероятность
 .
.
Количественная
мера информации
 (1.19) по аналогии с другими мерами будет
представлять в данном случае усреднение
частных мер количества информации
(1.20) при неполной достоверности результатов
опыта:
(1.19) по аналогии с другими мерами будет
представлять в данном случае усреднение
частных мер количества информации
(1.20) при неполной достоверности результатов
опыта:
 .
(1.21)
.
(1.21)
С учетом соотношений (1.13), соответствующих подстановок и преобразований, используемых в (1.14), из выражения (1.21) получим

откуда
находим (с учетом условия
 )
количество информации, в среднем
приходящееся на один опыт при его
неполной достоверности,
)
количество информации, в среднем
приходящееся на один опыт при его
неполной достоверности,
 ,
(1.22)
,
(1.22)
где
 – условная энтропия, характеризующая
потерю информации из-за недостоверности
результатов опыта.
– условная энтропия, характеризующая
потерю информации из-за недостоверности
результатов опыта.
Учитывая две формы записи (1.13) вероятности совместных событий для введенной меры количества информации, наряду с (1.22) нетрудно получить дополнительные формы:
 ,
(1.23)
,
(1.23)
которые могут использоваться при вычислении количества информации.