
- •Вопрос 2.
- •Часть 1.Количественная мера информации для равновозможных событий
- •Часть 2. Мера р. Хартли
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6. Свойства энтропии источника дискретных сообщений
- •Вопрос 7. Энтропия источника совместных сообщений
- •Вопрос 8. Что такое условная энтропия?
- •Вопрос 9.
- •Вопрос 10. Свойства количественной меры информации при неполной достоверности результатов опыта.
- •Вопрос 11. Вычисление количественной меры информации для двоичного канала с помехами.
- •Вопрос 12. Как оценивается избыточность источника сообщений?
- •Вопрос 13.
- •Вопрос 23.
- •Вопрос 24. Приведите модель двоичного канала с шумами
- •Вопрос 25.
- •Вопрос26. Формула Шеннона для аналогового канала с шумами.
- •Вопрос 27. Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •Вопрос 28. Принципы помехоустойчивого кодирования. Кодовое расстояние.
- •Вопрос 29. Вероятность ошибочного приема кодовой информации для простого двоичного кода и для кода с исправлением ошибок кратности t.
- •Вопрос 30. Простейшие избыточные коды.
- •Вопрос 31. Групповой код Хемминга. Принципы построения. Синдром ошибки. Коды с обнаружением и исправлением ошибок. Код хемминга
- •Вопрос 32. Определение числа проверочных элементов.
- •Вопрос 33. Определение проверочных элементов, входящих в каждую группу. Исправляющая способность кода хемминга
1. Дайте определение информационной системы и информационного процесса. Приведите понятие информации.
В настоящее время получили широкое распространение информационные системы. Под информационной системой будем понимать такую систему, которая реализует и поддерживает информационный процесс.
Под информационным процессом будем понимать такой процесс, в котором присутствует хотя бы один из элементов: передача информации, ее прием, хранение, обработка, выдача пользователю .
Понятие «информация» является основополагающим для информационных систем. Проявляется информация всегда в материально-энергетической форме в виде сигналов, являющихся материальными носителями информации
Понятие об информации.
Понятие «информация» может быть истолковано как некоторая совокупность сведений, определяющих меру наших знаний о тех или иных событиях, явлениях или фактах.
В данном случае понятие «информации» можно трактовать как сведения, являющиеся объектом хранения, передачи и преобразования.
Вопрос 2.
Часть 1.Количественная мера информации для равновозможных событий
Источники информации могут быть дискретными и непрерывными. Дискретные источники имеют конечный набор различных состояний, а непрерывные – бесконечный (теоретически).
Сначала рассмотрим дискретные источники.
Под событием будем понимать состояние дискретного источника информации (объекта). Например, в двоичном канале как источнике информации имеют место два события (состояния), условно называемые нулевым и единичным. Нулевому соответствует состояние, когда по каналу передается нулевой символ («0»), а единичному – когда передается единичный символ («1»).
Обратим, прежде всего, внимание на то обстоятельство, что всякая информация может быть получена только в результате того или иного целенаправленного опыта (действия). Таким опытом может быть получение телеграммы, чтение книги, просмотр информационного табло с расписанием движения транспортных средств, измерение температуры, запуск на поверхность планеты Венера исследовательского аппарата и передача с него интересующих данных на Землю и т.д.
Чем можно охарактеризовать факт получения информации? Можно сказать, что во всех случаях до опыта на интересующий нас вопрос мы не можем ответить однозначно. Таким образом, до опыта имеет место бóльшая или меньшая неопределенность в исходе тех или иных событий. После опыта, в результате которого мы можем получить информацию об интересующих нас событиях, ситуация становится более определенной: на поставленный вопрос мы можем ответить либо однозначно, либо, по крайней мере, число возможных ответов уменьшится и, следовательно, уменьшится имевшая место до опыта неопределенность.
Рассмотрим
пример (из студенческой жизни с фольклорным
оттенком). Вы отправились сдавать
экзамен. До опыта (экзамена) для Вас
возможны 4 исхода (оценки): «отлично»,
«хорошо», «удовлетворительно»,
«неудовлетворительно» (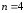 ).
Бабушка в томительном ожидании
обнаруживает, что Вы забыли телефон.
Тогда она обзванивает знакомых своей
внучки-студентки, пытаясь выяснить, как
она сдала экзамен. В результате такого
опыта (действия) она получает несколько
ответов на свой вопрос:
).
Бабушка в томительном ожидании
обнаруживает, что Вы забыли телефон.
Тогда она обзванивает знакомых своей
внучки-студентки, пытаясь выяснить, как
она сдала экзамен. В результате такого
опыта (действия) она получает несколько
ответов на свой вопрос:
– «Не знаю».
– «Неудовлетворительных оценок в группе не было».
– «Хорошо» или «Отлично».
– «Хорошо».
В
первом ответе исходная неопределенность
результат экзамена сохранилась ( ).
Во втором ответе неопределенность
уменьшилась до трех исходов (
).
Во втором ответе неопределенность
уменьшилась до трех исходов (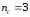 ).
В третьем ответе неопределенность еще
более уменьшилась до двух исходов (
).
В третьем ответе неопределенность еще
более уменьшилась до двух исходов (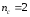 ).
В четвертом ответе неопределенность
оказалась исключенной: результат
экзамена (оценка) стал единственным (
).
В четвертом ответе неопределенность
оказалась исключенной: результат
экзамена (оценка) стал единственным (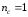 )
– «хорошо», что успокоило бабушку.
)
– «хорошо», что успокоило бабушку.
Из приведенного примера интуитивно следует, что полученные в результате проведенного опыта ответы будут содержать неодинаковое количество информации. Ее максимальное значение, очевидно, будет в четвертом ответе, когда ситуация полностью определяется и неопределенность результата экзамена полностью устраняется. Таким образом, уменьшение неопределенности в результате опыта (действия) может быть принято за наиболее общую меру количества получаемой информации. В этом смысле говорят, что информация обратна неопределенности. Чем больше устраняется неопределенность, тем больше мы получаем информации.
Все оценки количества информации основаны на понятиях теории вероятностей. Поэтому, прежде чем перейти к рассмотрению мер количества информации, познакомимся с элементами теории вероятностей, необходимыми для понимания рассматриваемого в данном курсе материала. Более подробно и строго теорию вероятностей вы будете изучать в следующем семестре в курсе «Математика».
Выше мы отметили, что дискретный источник информации может находиться в одном из конечного множества состояний. Это состояние мы назвали событием.
Пусть источник информации выдает последовательность n-разрядных цифровых слов, т.е. слов, состоящих всего из двух символов: 0 и 1. Обозначим событие, соответствующее появлению в i-м разряде слова «нуля» через А, а событие, соответствующее появлению «единицы» через В. Пусть в цифровом слове имеется m1 «нулей» и m2 «единиц». Очевидно, что m1+ m2=n.
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие.
Вероятность события А обозначают через р(А) (здесь р - первая буква французского слова probabilite - вероятность).
В соответствии с определением и принятыми обозначениями вероятность появления «нуля», т.е. события А, определяется как отношение числа элементарных исходов, благоприятствующих событию А (в нашем случае это число m1), к числу всех возможных элементарных исходов опыта (в нашем случае это число n):
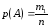
Соответственно,
 .
.
Это определение вероятности называют классическим. Оно возникло на начальном этапе развития теории вероятностей.
Вероятность события имеет следующие свойства:
1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой U. Для достоверного события m1=n, (т.е. для нашего примера цифровое слово состоит из одних «нулей», и какой бы разряд мы не выбрали, все равно получим 0).
Таким образом, р(U)=1.
2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой V. В нашем примере m1=n, соответственно m2=0, поэтому р(V)=0.
3. Вероятность случайного события выражается положительным числом, меньшим единицы 0<p(Х)<1.
4. Вероятность любого события Y удовлетворяет неравенствам 0≤p(Y)≤1.
