zadanie_1

Задание 1

Даны координаты вершин пирамиды 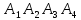. Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью; 4) площадь грани ; 5) объём пирамиды; 6) уравнение прямой ; 7)уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

15.

Решение:

Для дальнейшего решения найдем вектора по координатам точек и длины этих векторов (модули векторов):

1. Длина ребра равна длине вектора , а длину вектора мы уже нашли

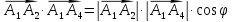
2. Угол между ребрами и найдем при помощи формулы скалярного произведения векторов: Найдем скалярное произведение векторов при помощи координат: Длины векторов уже найдены: Подставим значения в формулу

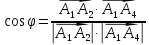
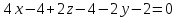
3. угол между ребром и гранью; Составим каноническое уравнение прямой : Направляющий вектор прямой имеет вид Найдем уравнение плоскости (тем самым выполним пункт 7). Для составления уравнения плоскости используем формулу: Вектор нормали плоскости имеет вид Найдем угол между прямой и плоскостью по формуле: где (координаты вектора ), (координаты вектора )

4. Площадь грани найдем при помощи векторного произведения векторов

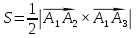
5. Объём пирамиды найдем через смешанное произведение векторов:

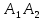6. уравнение прямой : Составим параметрическое уравнение прямой где – направляющий вектор прямой, в качестве которого можно взять вектор – координаты точки, лежащей на прямой, в качестве которых можно взять координаты точки Составим каноническое уравнение прямой Составим каноническое уравнение прямой :

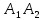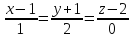
7. Уравнение плоскости (решено в пункте 3) Для составления уравнения плоскости используем формулу:

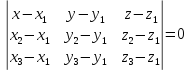
8. уравнение высоты, опущенной из вершины на грань нормальный вектор плоскости является направляющим вектором прямой

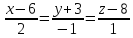
9. Чертеж: