Добавил:

qweru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Тепломассообмен

Файл:

ИТАЭ ТФ-10 9 семестр / Газодинамика / Конспект лекций.pdf

Скачиваний:

259

Добавлен:

30.12.2018

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 245 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

2.3 Механизм образования скачков уплотнения

Всякое повышение давления, возникающее в газовой среде, распространяется в ней в виде пакета волн давления. Слабые волны давления распространяются со скоростью звука. Однако, что особенно важно, это местная скорость звука, определяемая параметрами в данной области, где распространяется звуковая волна. Из этого факта следует, что если небольшие скачки давления следуют один за другим, то каждый последующий скачок движется по газу, сжатому предыдущим. Это означает, что температура этого газа выше, а скорость звука – больше, чем перед предыдущим скачком. Таким образом, задний скачок давления движется быстрее предыдущего, то есть догоняет его. Таким образом форма распространяющихся импульсов давления обязана меняться по времени и они будут стремиться слиться в один мощный импульс (скачок уплотнения или, иначе, ударную волну).

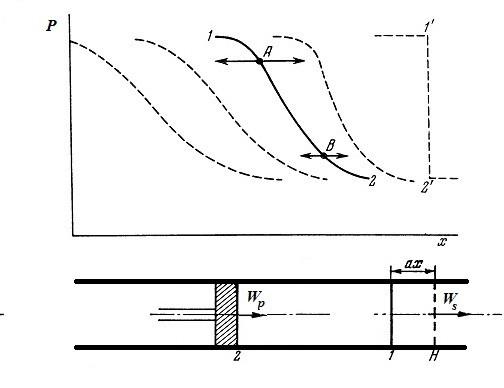
Такой сценарий, например, реализуется в случае газа, движущегося перед поршнем, который в момент времени t = 0 пришел в движение (рис.2.3.1). На рисунке волна в точке A бежит по уже сжатому, нагретому газу, то есть быстрее, чем волна в точке B.

Рисунок 2.3.1. Образование ударной волны перед поршнем и области разрежения за ним

Если же в газе происходит понижение давления, как например, в области за движущимся поршнем, то всякое понижение давления, возникающее в газовой среде, также распространяется в ней в виде пакета волн разрежения. Слабые волны разрежения также распространяются со скоростью звука. Это, разумеется, местная скорость звука, определяемая параметрами в данной области, где распространяется звуковая волна. Из этого факта следует, что если небольшие сбросы давления следуют один за другим, то каждый последующий сброс давления движется по газу, уже несколько разреженному предыдущим. Это означает, что температура этого газа ниже, а скорость звука – меньше, чем перед предыдущим сбросом давления. Таким образом, задняя волна разрежения движется медленнее предыдущей, то есть отстает от нее. Вследствие этого форма распространяющихся сбросов давления также обязана меняться по времени. Однако области, где происходит падение давления, будут все более и более растягиваться в пространстве.

Данные рассуждения не означают, что скачков разрежения не существует в принципе. Они возникают в случае, если местная скорость звука за фронтом волны разрежения больше, чем перед ним. Это возможно, если, например, за фронтом разрежения происходит нагрев газ. Именно этот эффект может наблюдаться в скачках конденсации и на фронте горения.

2.4 Прямые скачки уплотнения. Ударная адиабата

Рассмотрим простейшую теорию ударных волн на примере ударной волны, образующейся перед фронтом поршня, движущегося в трубе, достаточно широкой, чтобы пренебречь потерями на трение и другими эффектами, связанными с влиянием стенок. В данном случае фронт волны перпендикулярен направлению его движения, такие волны называются

прямыми ударными волнами (или, что то же самое, прямыми скачками). Пусть Wp – скорость поршня, эту же скорость имеет и газ за ударной

волной; Ws – скорость образовавшейся перед ним ударной волны, рис. 2.3.1. Здесь P1, T1, ρ1 – давление, температура и плотность за фронтом ударной волны; P2, T2, ρ2 – перед фронтом.

Выделяем в трубе участок длиной dx, ударная волна проходит его за время dτ, dx = Ws dτ . После прохождения ударной волны, масса газа в нем меняется на величину dG,

dG = ρ1 Wp dτ = (ρ1 – ρ2) dx = (ρ1 – ρ2) Ws dτ .

Отсюда следует, что

			22
W p=	ρ 1−ρ2	W s .	(2.4.1)

	ρ1

Так как ранее покоящийся на участке dx газ массой ρ2 dx далее начинает двигаться со скоростью Wp , то баланс импульса запишется в виде

ρ2 Wp dx = (P1 – P2) dτ .					(2.4.2)
Отсюда и из (2.4.1) получаем для скорости движения ударной волны

W s=√	P1−P2	√	ρ1
				.	(2.4.3)
	ρ1−ρ2		ρ 2

В случае слабой ударной волны она движется со скоростью звука,

Ws≈√∂∂ Pρ =aS .

Вобщем случае, как следует из (2.4.3), Ws > aS .

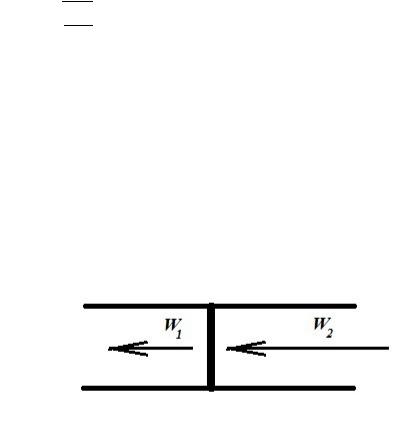
Для того, чтобы по формуле (2.4.3) определить скорость ударной волны, необходимо знать не только давление за ее фронтом, но и плотность газа за фронтом волны. Связь между этими величинами за фронтом ударной волны называется ударной адиабатой, по аналогии с обычной газовой адиабатой. Чтобы определить эту зависимость, рассмотрим ударную волну в системе координат, движущейся вместе с фронтом ударной волны, рис. 2.4.1.

Рисунок 2.4.1. Ударная волна в собственной системе координат

Пусть в данной системе координат W1 = Wp - Ws – скорость газа за ударной волной; W2 = - Ws – скорость газа перед ударной волной. Уравнение неразрывности принимает вид

ρ1 W 1=ρ 2 W 2=G=const .

(2.4.4)

Так как через фронт ударной волны в секунду проходит масса газа G, уравнение сохранения количества движения имеет вид

P1−P2=G (W 2−W 1)=W 1 W 2 (ρ 1−ρ 2)=ρ 2 W 22−ρ1 W 12 .

(2.4.5)

При прохождении газом через фронт ударной волны его полная энтальпия (см. п. 1.4, формула (1.4.4)) обязана сохраняться. Для идеального газа, у которого теплоемкость постоянна, из (1.4.4) следует, что

W 2

−

2CP

2 C P

В таком случае

P1−P2=ρ 1 RT 1−ρ 2 R T 2=(ρ1−ρ 2) R T 0+

(ρ2 W 22−ρ1 W 12) .

(2.4.6)

2C P

С учетом (2.4.5) получаем

P1−P2=(ρ1−ρ 2 )R T 0+

(C P−CV )

(P1−P2 ) .

2C P

Окончательно

P1−P2

2 k

2 2

W 1 W 2=

R T 0=

a0=acrit .

(2.4.7)

ρ 1−ρ 2

k+1

Напомним, что acrit – скорость звука в критическом сечении , a0 – скорость звука при параметрах полного торможения. Вспомнив также

определение коэффициента скорости	λ =	W	, перепишем соотношение
определение коэффициента скорости	λ =	acrit	, перепишем соотношение
		acrit
(2.4.7) в форме, в которой оно было получено Л. Прандтлем, 1924,
λ1 λ2=1 .			(2.4.8)

Из (2.4.8) следует, что если поток газа, входящий в ударную волну, является сверхзвуковым (λ2 > 1), то проходя фронт волны этот поток становится дозвуковым (λ1 < 1).

Аналогично (2.4.6) получаем

P1+P2=ρ 1 RT 1+ρ 2	RT 2=(ρ1+ρ 2) RT 0−	k−1	(ρ 2 W 22+ρ1W 12)	. (2.4.9)
		2 k

					24
Так как из (2.4.4), (2.4.5) следует, что
ρ 2W 22+ρ 1 W 12=W 1 W 2					(ρ 1+ρ 2)=	P1−P2	(ρ 1+ρ 2) ,

						ρ1−ρ 2
с учетом соотношения (2.4.7) из (2.4.9) получаем
k	P1+P2		P1−P2
		=		.	(2.4.10)
	ρ1+ρ 2		ρ 1−ρ 2

Данное соотношение и является ударной адиабатой, так как устанавливает связь между плотностью и давлением газа за ударной волной. Так как впервые данное соотношение было получено П. Гюгонио, 1885, то оно часто называется адиабатой Гюгонио.

Выражение (2.4.10) также может быть записано в виде

			k+1		+	P2
ρ1	=		k−1		+	P1		.	(2.4.11)
ρ2	=	1+		k+1 P			2	.	(2.4.11)
ρ2				k+1 P			2

				k−1 P1
				k−1 P1

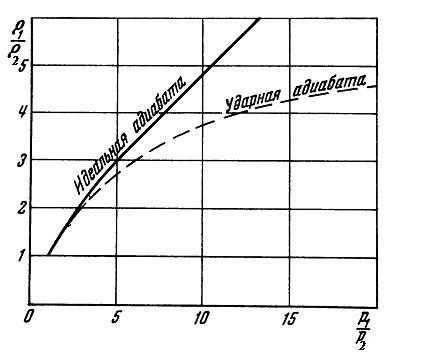
На рис. 2.4.2 для воздуха (k = 1.4) приведены как ударная адиабата (2.4.11), так и адиабата идеального газа (изоэнтропа)

ρ1		P1		1
				k
	=(		)	.
ρ2		P2

Для идеального газа, сжимаемого по адиабате, при давлении P1 → ∞ также и плотность газа ρ1 → ∞ . В отличие от идеальной адиабаты, в ударной адиабате при P1 → ∞ отношение плотностей газа за ударной волной и перед ударной волной стремится к постоянной величине

ρρ12 →( kk+−11) . Для воздуха это отношение равно 6.

Рисунок 2.4.2. Адиабата идеального газа (изоэнтропа) и ударная адиабата для воздуха

Определим связь между интенсивностью ударной волны

и ее

W 2

числом Маха

M 2=

, где a2 – скорость звука перед фронтом ударной

волны,

a22=k

. Для этого перепишем (2.4.5) в виде

ρ 2

(

−1)k

ρ 2

W 2 W 2(

ρ1

−1) .

ρ 2

ρ 1

ρ 2

Выражая отношение плотностей через отношение давлений в соответствии с (2.4.11) окончательно получаем

P1		2 k	2	k −1
	=		M 2−		.	(2.4.12)
P2	=	k+1	M 2−	k +1	.	(2.4.12)
P2		k+1		k +1

Определим, является ли процесс прохождения газом ударной волны изоэнтропным. Для этого определим значения удельной энтропии газа за скачком s1 и перед ним s2 .Так как изменение энтропии

<<< < Предыдущая 1 2 3 45 / 245 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>