97
П6. Прямоточный воздушно-реактивный двигатель (ПВРД)
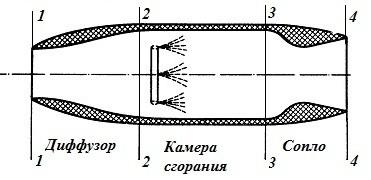
Установим взаимосвязь между скоростью полета и скоростью истечения из прямоточного воздушно-реактивного двигателя (ПВРД), схема которого изображена на рис. П6.1. Во входном участке двигателя происходит преобразование скоростного напора набегающего потока в давление, то есть динамическое сжатие воздуха. В камере сгорания подводится тепло, и образующаяся смесь сжатого воздуха с продуктами сгорания нагревается. В выходном сопле нагретые газы расширяются: здесь давление преобразуется в скоростной напор (Б. С. Стечкин, 1929).
Рисунок П6.1. Схема прямоточного воздушно-реактивного двигателя (ПВРД)
Наиболее совершенный цикл работы прямоточного воздушнореактивного двигателя был бы получен в том случае, если бы сжатие воздуха на участке 1 – 2 (рис. П6.1) осуществлялось по идеальной адиабате и скорость потока была бы доведена до нуля, подвод тепла в камере сгорания 2 – 3 происходил бы при постоянном давлении, после чего выхлопная смесь расширялась бы в сопле 3 – 4 до атмосферного давления также по идеальной адиабате. Прямоточный воздушно-реактивный двигатель, работающий по указанному совершенному циклу, называют идеальным.
Полное давление P0 в камере сгорания может быть найдено из уравнения Бернулли (1.5.1), которое в случае идеальной адиабаты имеет вид:
k |
|
P1 |
|
P0 |
|
k−1 |
|
W |
2 |
|
|
[( |
) |
k |
−1]= |
1 |
. |
||||
k −1 |
|
ρ 1 |
P1 |
|
2 |
|
||||
|
|
|
|
|
|
|
Скорость истечения найдется из аналогичного выражения при P4 = P1
k |
|
P1 |
|
P0 |
|
k−1 |
|
W |
2 |
|
|
[( |
) |
k |
|
−1]= |
4 |
||||
k −1 |
|
ρ 4 |
P1 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
||||
98
Отсюда мы получаем основное соотношение
|
W |
2 |
|
W |
2 |
. |
ρ1 |
|
1 |
=ρ4 |
|
4 |
|
2 |
|
2 |
|
Итак, в идеальном прямоточном воздушно-реактивном двигателе скоростной напор потока в выхлопном отверстии равен скоростному напору полета. Используя это же равенство, получим для идеального двигателя P01 = P02, Р1 = Р4) еще один важный результат: λ1 = λ4, то есть приведенные скорости в выходном отверстии идеального двигателя и в набегающем невозмущенном потоке равны. Отсюда вытекает также и равенство чисел Маха полета и истечения М1 = М4.
Эти соотношения справедливы для идеального двигателя как при додозвуковой, так и при сверхзвуковой скорости полета.
Полученные соотношения приводят к простой расчетной формуле для скорости истечения в идеальном двигателе, связывающей для идеального двигателя скорость истечения с отношением температур торможения, взятых в конце (T04 ) и начале (T01) камеры сгорания:
W 4=W 1 √ |
|
ρ1 |
=W 1 √ |
|
T 04 |
|
||
|
|
|
. |
|||||
ρ 4 |
T 01 |
|||||||
Для идеального двигателя температура торможения в начале камеры сгорания совпадает с температурой полного торможения исходного потока газа T0 = T01, а температура полного торможения в конце камеры сгорания T04 либо задается по закону регулирования двигателя, либо может
быть посчитана по соотношению |
T 04 |
=T 01 |
+ |
q |
, где q – количество |
|
|||||
|
|
|
|
C P |
|
тепла, переданное одному килограмму газа.
99
П.7. Одномерное стационарное течение газа по трубе постоянного сечения с подогревом
Задача: На малом участке длины трубы к стационарно текущему по ней газу подводится небольшое количество тепла. Определить изменение скорости газа при прохождении им этого участка. Газ предполагается политропным.
Решение: Пусть Sq есть подводимое в единицу времени количество тепла (S — площадь сечения трубы в данном ее участке). На обеих сторонах участка подогрева одинаковы плотности потока массы j = ρW и потока импульса P + jW; отсюда ΔP = -j ΔW, где обозначает изменение величины при прохождении этого участка. Разность же плотностей потока энергии (h +W2/2) j равна q. Написав энтальпию h в виде
h= |
k P |
k P W |
||||
|
= |
|
, |
|||
(k −1)ρ |
(k −1) j |
|||||
получим, считая ΔW и ΔP малыми, |
||||||
q=W j W + |
k |
(P W +W P) . |
||||
k −1 |
||||||
|
|
|
|
|
||
Исключая ΔP из этих двух соотношений, найдем:
W(k −1)q
=ρ (a2−W 2) .
Мы видим, что при дозвуковом течении подвод тепла ускоряет поток (ΔW > 0), а при сверхзвуковом – замедляет.
Написав |
температуру газа в виде |
|
T = |
μ P |
= |
μ P W |
(R – газовая |
||||||
|
ρ R |
j R |
|||||||||||
постоянная), найдем для ее изменения выражение |
|
|
|
||||||||||
|
μ |
|
μ(k−1)q a2 |
|
2 |
|
|
|
|
||||
T = |
|
(W P+P W )= |
|
( |
|
−W |
|
) . |
|
|
|||
R j |
R j(a2−W 2) |
k |
|
|
|
||||||||
При сверхзвуковом движении это выражение всегда положительно – температура газа повышается; при дозвуковом же движении оно может быть как положительным, так и отрицательным.
100
П.8. Адиабатическое течение газа с трением в трубе постоянного сечения
Задача: Определить, как меняются параметры газового потока при его стационарном течении в круглой трубе длиной L , с постоянным сечением S при наличии трения.
Решение: В соответствии с результатами, полученными в п. 2.10, изменение параметров газа по длине трубы описывается уравнением
(M 2−1) dW |
=− |
k |
dL fric , |
(П8.1) |
2 |
||||
W |
|
a |
|
|
где dLfric – тепло, выделяемое в одном килограмме газа в результате процессов трения. Так как dLfric > 0 всегда, то трение ускоряет дозвуковой поток, а сверхзвуковой – замедляет. Непрерывный переход через скорость звука в трубе постоянного сечения оказывается невозможным и M = 1 может достигаться только в выходном сечении трубы. На длине dx трубы сечением S и периметром Π = πD в одном килограмме газа выделяется тепло
d L fric= |
τ Π dx |
, |
|
|
|
ρ S |
ρ W 2 |
|
|||
|
|
|
|||
здесь τ – напряжения трения на стенке трубы, τ =ξ |
, ξ – |
||||
8 |
|||||
|
|
|
|
||
коэффициент гидравлического сопротивления. В таком случае уравнение (П8.1) принимает вид
(M |
2−1) dW =−ξ k |
M 2 |
dx . |
|
|
|
|
|
|
|
|
(П8.2) |
|||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
W |
|
|
D |
|
|
|
|
|
|
|
|
|
||||||
Удобно решать |
задачу |
|
выражая все параметры |
через |
коэффициент |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
2 |
λ |
2 |
|
|
|
скорости (см. п. 1.5) |
|
λ = |
|
, учитывая, что M 2= |
|
k+1 |
|
|
. |
||||||||||||
acrit |
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1− |
k−1 |
λ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение (П8.2) принимает вид |
k+1 |
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
( |
1 |
|
−1)d |
λ |
=ξ |
k |
|
dx . |
|
|
|
|
|
|
|
|
(П8.3) |
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
λ |
|
|
λ |
k +1 D |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интегрируя (П8.3) от входного (1) до выходного (2) сечений трубы получаем окончательное уравнение
|
|
|
|
|
|
101 |
|
||
φ (λ1 )−φ (λ2)=χ . |
|
|
|
|
(П8.4) |
||||
Здесь |
функция |
φ (λ )= |
1 |
+2 ln λ |
, а |
приведенная длина трубы |
|||
2 |
|||||||||
|
k L |
|
λ |
|
|
||||
|
|
|
|
|
|
||||
χ =ξ |
|
|
|
. |
|
|
|
|
|
k +1 |
D |
|
|
|
|
|
|||
Уравнение (П8.4) позволяет определить параметры потока на выходе из трубы, зная коэффициент скорости газового потока на входе. Следует отметить, что стационарное решение данного уравнения для дозвуковых потоков возможно только при χ <φ (λ1)−1 . Для сверхзвуковых потоков
условие χ >φ (λ1)−1 приводит к возникновению скачка уплотнения внутри трубы.