93
П3. Пример расчета аэродинамического нагрева
Задача: Сверхзвуковой самолет-разведчик SR-71 в крейсерском режиме летит со скоростью около W = 1000 м/с. Определить температуру воздуха вблизи его переднего носка крыла и температуру самого крыла.
Решение: Так как воздух вплоть до температур около 2000 К имеет практически постоянную теплоемкость CP = 1000 Дж/кг К, то температуру полного торможения, которую принимает воздух вблизи носка крыла, можно определить из (1.4.4) как
T 0=T + |
W 2 |
=T + |
W 2 |
. |
|
2000 |
|||
|
2CP |
|
||
Здесь T – температура воздуха в окружающем самолет пространстве (как обычно говорят – в набегающем потоке). При T = 300 K температура полного торможения составит T0 = 800 К.
Установившаяся температура TS для поверхности, которая контактирует с высокоскоростным потоком, (ее называют температурой адиабатической стенки) обычно несколько меньше, чем температура полного торможения, которую принимает газ, останавливаясь вблизи стенки. Ее определяют по формуле, аналогичной (1.4.4), вводя поправочный коэффициент φ (надежно определяется только опытным путем)
T S =T +φ |
W 2 |
. |
|
||
|
2CP |
|
Для для дозвуковых скоростей φ ~ 0.8, для сверхзвуковых скоростей φ ~ 0.5. В данном случае температура носка крыла составит 550 К (277 С). Как видим, аэродинамический нагрев конструкции высокоскоростных летательных аппаратов весьма значителен. Именно поэтому детали летательных аппаратов, вблизи которых происходит торможение газовых потоков (носки крыла, киль и стабилизаторы и др. ) приходится выполнять из жаропрочных материалов. Отличие температуры адиабатической стенки как от температуры в набегающем потоке, так и от температуры полного торможения, следует учитывать при прямых измерениях температуры высокоскоростных потоков.
94
П4. Гидравлический удар при внезапной остановке потока жидкости
Задача: Определить давление, возникающее в водяном потоке, движущемся со скоростью Wp = 1 м/с при его внезапной остановке.
Решение: При резкой остановке потока жидкости возникает ударная волна, которая в жидкости, в связи с ее слабой сжимаемостью, распространяется практически со скоростью звука а, в то время как плотность за и до ударной волны остается фактически постоянной. Уравнение баланса импульса (2.4.2) для параметров за и перед ударной волной в таком случае принимает вид
P1 – P2 = ρ Wp a.
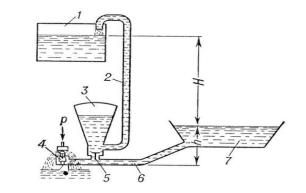
Для воды с ρ=1000 кг/м3 , а = 1800 м/с получаем P1 – P2 = 1.8 МПа. Данное явление носит название гидравлического удара. Гидравлический удар часто возникает в технике при быстром закрытии регулирующих задвижек, при остановке турбин и насосов. Данное явление может вызвать разрушение стенок и стыков трубопроводов, частей машин и приборов. Основанные на использовании гидравлического удара насосы (гидравлические тараны, рис. П4.1.) способны подымать жидкость на значительную высоту, а гидравлические турбины – работать на небольших низконапорных реках.
Рисунок П4.1. Гидравлический таран: 1 – верхний бак; 2 – отводящая труба; 3 – воздушный колпак; 4 – отбойный клапан; 5 – возвратный клапан; 6 – питающая труба; 7 — напорный бассейн
Данная задача призвана проиллюстрировать, что в механике жидкости и газа стационарная и нестационарная задачи могут дать радикально различающиеся результаты. Ведь если для расчета давления использовать интеграл Бернулли (1.4.5), который применим только для стационарного течения, то мы получим лишь P1 – P2 = 500 Па, что соответствует подъему жидкости на мизерные 5 см.
95
П5. Трубка Пито при сверхзвуковом движении газа
Для измерения скорости сверхзвукового газового течения можно пользоваться обычным пневматическим насадком (рис. П5.1), иначе называемым трубкой Пито. Нужно только учесть, что при сверхзвуковом обтекании насадка перед ним возникает ударная волна. Если ось симметрии насадка параллельна направлению потока, то центральная газовая струйка, претерпевающая полное торможение, сначала проходит через прямую часть ударной волны, где ее скорость становится дозвуковой, затем при подходе к отверстию 1 скорость плавно уменьшается до нуля.
Давление P01 в трубке 1 может быть вычислено следующим способом. Из выражения (1.5.4) имеем
P01 |
=(1+ |
k −1 |
M 1 |
2 |
|
k |
|
|
)k−1 . |
||||||||
P1 |
2 |
|
||||||
|
|
|
|
|
|
|||
где P1 и M1 — статическое давление и число Маха непосредственно за ударной волной. Используя формулу (2.4.7), переходим к числу М в набегающем потоке:
1+ |
k −1 |
M 2 |
|
||||
|
|
||||||
M 12= |
|
2 |
|
|
|
. |
|
|
|
k−1 |
|||||
2 |
|
|
|||||
|
k M |
− |
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
96
Рисунок П5.1. Трубка Пито в сверхзвуковом потоке: 1 – отбор давления полного торможения; 2 – отбор статического давления.
Отсюда на основании равенства (2.4.12) получаем формулу, выражающую отношение давления P01 в трубке 1 к статическому давлению в набегающем потоке P как функцию числа М в набегающем потоке:
P01 |
|
k +1 |
|
k+1 |
|
2 |
|
1 |
|
|
|
M |
2k |
|
||||
|
|
|
|
|
|
|
k−1 |
|
|
|
|
|||||||
=( |
)k−1( |
)k−1 |
|
|
. |
|||||||||||||
P |
2 |
k −1 |
|
2 k |
|
|
1 |
|
||||||||||
|
|
|
|
( |
|
M 2−1)k −1 |
||||||||||||
|
|
|
|
|
|
|
k−1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для воздуха (k = 1.4) эта формула приводится к следующему виду:
P01 |
|
166.7 M 7 |
|
|
= |
|
. |
P |
(7 M 2−1)2.5 |
||
Статическое давление P1 в потоке за ударной волной, фиксируемое в трубке 2, определяется через число Маха набегающего потока соотношением (2.4.12), которое в данном случае имеет вид
P1 |
|
2 k |
2 |
|
k−1 |
. |
|
|
= |
|
M |
− |
|
||
P |
k +1 |
k+1 |
|||||
|
|
|
|
Знание величин P1 и P01 позволяет определить число Маха набегающего потока.