67
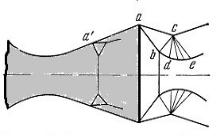
Рисунок 4.1.7. Истечение из сопла Лаваля при сильном перерасширении; abc
– мостообразный скачок на срезе сопла; a' – скачок внутри сопла, вызывающий отрыв потока
4.2Дозвуковые и сверхзвуковые диффузоры
Вдиффузорах происходит преобразование кинетической энергии потока газа в его внутреннюю энергию с минимальным, по возможности, ростом энтропии. В идеальном диффузоре торможение газа происходит изоэнтропно. Такой процесс торможения можно осуществить, в соответствии с законом обращения воздействий (2.10.3), отводом или подводом: тепла, массы , механической энергии и изменением проходного сечения канала.
Соответственно различаются следующие типы диффузоров:
•тепловые;
•расходные;
•механические;
•геометрические.
По значению числа Маха на входе:
•дозвуковые;
•околозвуковые;
•сверхзвуковые.
Наиболее распространены дозвуковые геометрические диффузоры, которые подразделяются на:
•плоские;
•конические;
•кольцевые;
•осерадиальные.
68
Эффективность диффузора определяют коэффициентом полного
давления |
P0,3 |
, где P0,1, P0,3 – давление полного торможения в |
σ = P0,1 |
набегающем потоке и на выходе из диффузора соответственно.
Дозвуковые геометрические диффузоры:
Возможные конфигурации струи перед дозвуковым геометрическим диффузором изображены на рис. 4.2.1.
Какой из трех случаев, изображенных на рис. 4.2.1, реализуется – определяется расходом газа через диффузор. Как показывает эксперимент, наиболее выгоден случай W2 ~ 0.5 W1 .
Рисунок 4.2.1. Возможные конфигурации струи перед диффузором: а – внешнее частичное торможение потока; б – вход в диффузор без изменения параметров; в – с внешним ускорением потока
Течение газа в диффузоре характеризуется положительными градиентами давления, что создает предпосылки для интенсивного нарастания пограничного слоя и отрыва потока от стенки. Последнее вызывает интенсивную диссипацию кинетической энергии набегающего
69
потока и приводит уменьшению давления полного торможения на выходе из диффузора.
Потери полного давления в диффузорах принято разделять на потери на трение в пограничном слое и потери на расширение. Последние, фактически, и являются потерями на образование вихрей в диффузоре при отрыве потока.
Потери на трение рассчитываются стандартным образом через коэффициент гидравлического сопротивления ξ. Обычно эти потери весьма малы. Потери же на вихреобразование определяют следующим образом.
При внезапном расширении канала поток резко замедляется, претерпеваю своеобразный удар. Потери полного давления в таком случае составляют (см. приложение П1)
Pstrike=ρ |
(W 2−W 3)2 |
. |
(4.2.1) |
|
2 |
||||
|
|
|
Для диффузора данную формулу модифицируют, вводя величину ψ – коэффициент полноты удара,
P0,1−P0,3=ψ Pstrike=ψ ρ |
(W 2−W 3 )2 |
. |
(4.2.2) |
|
2 |
||||
|
|
|
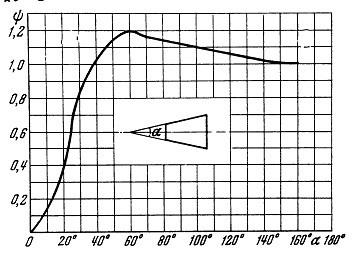
Экспериментальная зависимость коэффициента полноты удара от угла раскрытия диффузора приведена на рис. 4.2.2. Суммарная зависимость коэффициента полного давления от числа Маха на входе в диффузор показана на рис. 4.2.3.
Рисунок 4.2.2. Зависимость коэффициента полноты удара от угла раскрытия диффузора
70
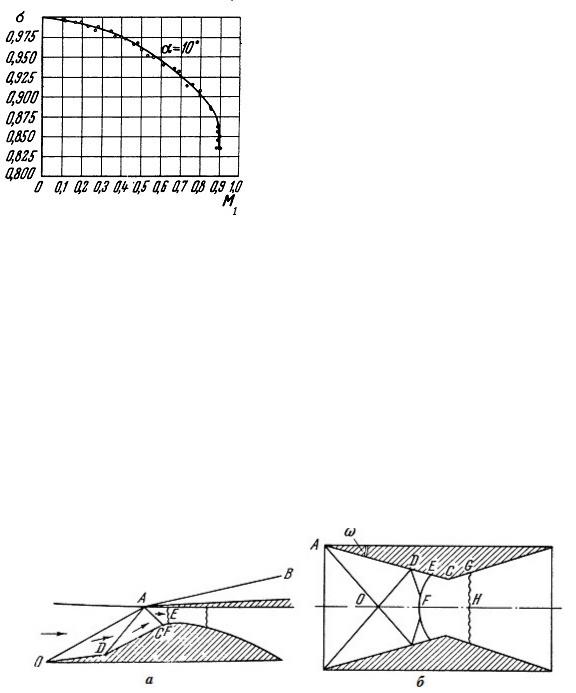
Рисунок 4.2.3. Зависимость коэффициента полного давления от числа Маха на входе в диффузор
Сверхзвуковые геометрические диффузоры:
Сверхзвуковой поток, претерпевающий замедление, неустойчив к образованию ударных волн, поэтому диффузоры, в которых торможение потока пытаются производить без генерации ударных волн (изоэнтропийные диффузоры) применяются в технике достаточно редко. Весьма распространенным приемом, предложенным К. Осватичем, является торможение потока газа в последовательности слабых косых ударных волн с завершающим прямым скачком уплотнения, как показано на рис. 4.2.4.
Рисунок 4.2.4. Сверхзвуковые геометрические диффузоры: а – с частичным внешним сжатием; б – с внутренним сжатием
На рис. 4.2.4а: ОА – первый косой скачок, DA – второй косой скачок, CA – прямой завершающий скачок, AB – косой скачок внешнего обтекания.
На рис. 4.2.4б: AO, OD, DF – система косых скачков, EF – завершающий мостообразный скачок.
71
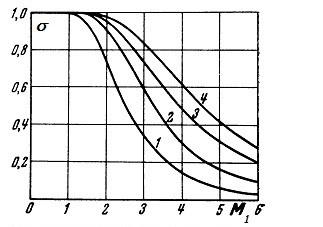
Рисунок 4.2.5. Зависимость оптимального коэффициента сохранения полного давления от числа Маха набегающего потока в системах из n скачков уплотнения: (n-1) – косых скачков + прямой завершающий скачок
Зависимость оптимального коэффициента полного давления от числа Маха набегающего потока в системах из n скачков уплотнения, среди которых (n-1) – косых скачков и прямой завершающий скачок, приведена на рис. 4.2.5.