Вопрос 13. Понятие локального экстремума. Необходимое условие локального экстремума.

U = f(x₁, x₂, …, x_n) опр. в окрест. точки М₀(х₁⁽⁰⁾, …, х_n⁽⁰⁾)

Опр.: Ф-я U = f(x) имеет в точке М₀ локальный максимум (минимум), если сущ. окр. точки М₀, в которой f(M₀) явл. наибольший (наим.) значением, среди всех значений f(M).

Опр.: Точка М₀ явл. точка лок. экстремума, если точка М₀ – точка лок. максимума или лок. минимума.

Утв. (необходимое условие лок. экстремума ф-ции неск. переменных) Если f=U(x₁, …, x_n) имеет в точке М₀(х₁, …, х_n) лок. экстремум и сущ. ∂f/∂x_i(M₀), i=1,…,n, то ∂f/∂x_i(M₀)=0, i=1,…,n

Док-во:∂f/∂x₁(M₀)=0, f=U(x₁⁽⁰⁾, …, x_n⁽⁰⁾) имеет экстремум => (dU(x₁,x₂⁽⁰⁾,…,x_n⁽⁰⁾)/dx₁|_x1(0) =0, ∂U/∂x₁(x₁⁽⁰⁾, …, x_n⁽⁰⁾)= dU(x₁, x₂⁽⁰⁾, …x_n⁽⁰⁾)/dx₁|_x1(0)=0

Утв. (необходимое условие локального экстремума ф-ции нескольких переменных) Если f=U(x₁, …, x_n) имеет в точке М₀(x₁⁽⁰⁾, …x_n⁽⁰⁾) лок. экстремум и диффер. в точке М₀, то dU|_M0=0.

Вопрос 14. Достаточное условие локального экстремума.

Пусть ф-ция , , дважды непрерывно дифференцируема в окрестности своей критической т. x⁽⁰⁾. Тогда если второй дифференциал ф-ция f явл. положит.(отрицат.) определённой квадратичной формой, то x⁽⁰⁾ есть т. строгого min(max). Если второй дифференциал – знакопеременная квадратичная форма, то в т. x⁽⁰⁾ экстрем. нет.

Согласно формуле Тейлора для приращения ф-ции , , в силу определения критичесткой т. получим , (1)

где , (2). Положим . квадратичная форма переменных.

Из (1) при имеем (3). Здесь и, т. лежит на еденичной сфере . Рассмотрим два случая.

1. Если – знакоопределённая квадратичная форма, то . Поскольку , то для всех выполняется неравенство (4), а в силу условия (2) такое , что для всех, для которых , имеет место неравенство (5). Из соотношений (3),(4) и (5) ,что для всех , , , знак приращения ф-ции совпадает со знаком квадратичной формы , и, если – положительно определённая квадратичная, форма, то , т.е. т. x⁽⁰⁾ является т. строгого минимума, а если – отрицательно определённая форма, то , т.е. т. x⁽⁰⁾ явл. т. строгого максимума.

2. Если – знакопеременная квадратичная форма, то такие и , что , (отсюда, очевидно, следует, что и , ибо ). Тогда для любого будем иметь и , в частности, , .

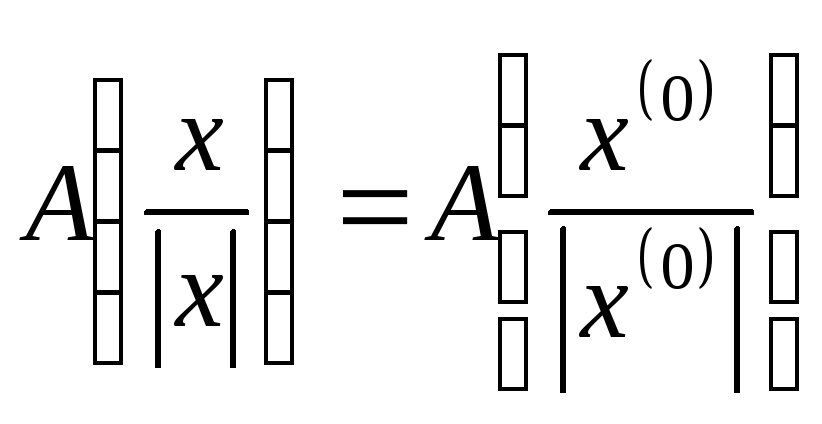(6) В силу условия(2) такое , что для всех , , имею место неравенства (7), (7). По этому для любой т. вида , , получим неравенство , а для т. вида , , – неравенство

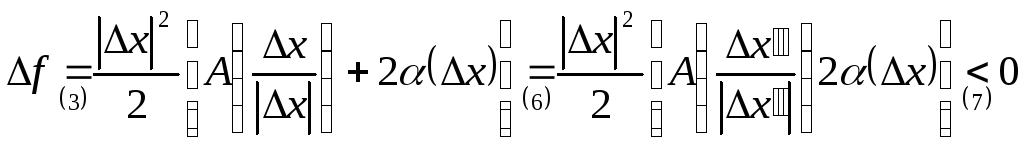
Поскольку среди указанных имеются сколь угодно малые по длине , то сколь угодно близкие к т. , для которых как , так и . Это и означает, что т. не является т. экстремума.

Вопрос 15. Понятие условного экстремума. Метод множителей Лагранжа. Необходимое условие условного экстремума.

Пусть на мн-ве задано ф-ций и пусть подмн-во мн-ва, на кот. последние ф-ций одновременно обращаются в нуль: . Уравнения (1) ур-я связи. Т. наз. т. условного экстремума ф-ции при выполнении условий связи (1), если она явл. т. обычного экстремума ф-ции на мн-ве .Пусть ф-ции непрерывно дифференцируемы в окр. т. . Если явл. т. условного экстремума ф-ции относительно ур-ий связи (1), то в этой т. градиенты линейно зависемы т.е. такие числа , одновременно не равные нулю, что .

Док-во: Пусть т. удовлетворяет уравнениям связи (1): (2) и в ней градиенты линейно независемы. Покажем, что в этом случае т. не может быть т. Усл. экстр.Если градиенты лин незав в т. , то в этой т. ранг матрицы (3) равен и, у этой матрицы минор порядка , не равный нулю. Пусть это будет минор, образованный первыми столбцами матрицы (3), т.е. (4). Рассмотрим отображение (5).

В силу выполнения уравнений связи (1) для т. имеем т.е. (5) отображает т. в т. . В силу же условия (4) отображение (5) отображает любую достаточно малую окрестность точки в пространстве переменных на некоторую окрестность точки . Поэтому для всех достаточно малых , а именно таки, что , отображение (5) отображает в точки и какие-то точки и из . Это означает, что для и выполняются соотношения (см.(5)) . Таким образом, т. и удовлетворяют уравнениям связи, причем в первой из них значение ф-ции больше , а во второй меньше. Поскольку произвольно малая окрестность т. , то это и означает, что т. не явл. т. условного экстремума ф- ции .

(Метод множителей Лагранжа). Пусть – независеммые вещественные переменные. Рассмотрим ф-цию Лагранжа . Для того чтобы неособая т. (т.е. ) ф-ции была бы т. условного экстремума этой ф-ции необходимо, чтобы при некотором имело место равенство т.е. чтобы все частные производные ф-ции по переменным и обращались в нуль.

Док-во: Если мы приравняем к нулю частные производные по переменным , то получим уравнения связи. А если продифференцируем по , то получим условие выражения градиента ф-ции в виде линейной комбинации градиентов ф-ций , что по теореме(см. предыдущую теорему) и явл. необходимым условием.0