6.3. Біном Ньютона. Властивості біноміальних коефіцієнтів.

Розглянемо двочлени вигляду (), перемножимо їх і зведемо подібні члени:

.

Очевидно, коефіцієнт множини є сумою добутків, кожен з яких утвориться -елементами з (-сполучення з елементів), причому в кожному таких добутків . Якщо покласти , то будь-який добуток -сполучень елементів дорівнює 1 і, отже, . Таким чином,

.

Цей вираз називається біномом Ньютона, а -сполучення з різних елементів є біномними коефіцієнтами.

За допомогою бінома Ньютона можна вивести різні формули для сполу­чень.

Приклад 6.11. Знайти кількість натуральних розв’язків рівняння

, де .

Кожний натуральний розв’язок рівняння представимо як суму одиниць кількість яких дорівнює : . Індексом у одиниці позначаємо її належність до розкладу числа . Таким чином, ми ввели різних типів одиниць, тобто різних типів елементів , причому кожне ().

Будь-який розв’язок рівняння можна представити як суму, що складена з довільних одиниць множини . Якщо ми додамо всі одиниці з однаковими індексами, то отримаємо відповідні складові розв’язку початкового рівняння. Дана відповідність є взаємно однозначною, тому кількість розв’язків рівняння дорівнює числу сполучень з повтореннями:

.

Нехай є множина з різних елементів. Розглянемо біномні коефіцієнти:

вказує скількома способами можна вибрати 0 елементів з , тобто створити 0-елементну підмножину множини ;

вказує скількома способами можна вибрати 1 елементів з , тобто створити 1-елементну підмножину множини ;

вказує скількома способами можна вибрати елементів з , тобто створити -елементну підмножину множини ;

вказує скількома способами можна вибрати елементів з , тобто створити -елементну підмножину множини .

А сума цих біноміальних коефіцієнтів дорівнює кількості способів створити всі підмножини множини . Задля того, щоб добути суму коефіцієнтів, треба щоб спів множини дорівнювали 1. Тому поклавши , матимемо . Ця формула визначає кількість усіх підмножин деякої множини.

При знаходимо .

6.4. Поліномні твірні функції.

Добуток породжує r-сполучення з n різних елементів, в яке кожний об’єкт із множин може входити не більш як один раз. Щоб одержати інші вигляди сполучень, треба брати й інший вигляд співмножників.

Якщо об’єкт може входити в сполучення разів, то замість потрібно взяти співмножник .

Тоді при коефіцієнти багаточлена будуть r-сполученнями з n різних елементів із повтореннями.

Приклад 6.12. Знайдемо за наведеною схемою для сполучення з трьох елементів зі специфікацією {3, 1, 2} добуток [1].

.

Тут коефіцієнт при дає шукане число n-сполучень, тобто:

3 – число 1-сполучень (це );

5 – число 2-сполучень(це );

6 – число 3-сполучень(це ).

Багаточлен називається поліномною твірною функцією (енумератором) для послідовності . У випадку, що розглядається, ця послідовність є r-сполученням з n елементів із повтореннями. Біном Ньютона, твірна функція для сполучень без повторень, є окремим випадком твірної функції загального вигляду. Слід мати на увазі, що змінна х енумератора ніяк не визначена і вважається просто абстрактним символом. Його роль зводиться лише до того, щоб розрізняти елементи послідовності . При цьому різні перетворення таких послідовностей замінюються відповідними операціями над твірними функціями.

Для сполучень із необмеженими повтореннями елементів n типів енумератором буде вираз , який можна записати у вигляді

.

Розглядаючи вираз як біном Ньютона з від’ємним показником , формально дістаємо

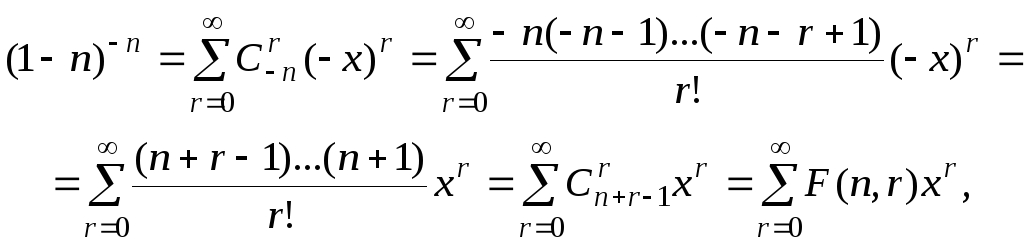
що збігається з раніше одержаним результатом.

Якщо потрібно визначити число r-сполучень з n типів елементів із необ­меженими повтореннями, яке обов’язково містить хоча б один елемент кожного типу, то енумератор

.