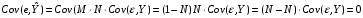- •2.Автокорреляция случайного возмущения. Причины. Последствия.
- •4.Автокорреляция. Методы устранения автокорреляции
- •5.Алгоритм проверки адекватности парной регрессионной модели
- •6.Алгоритм проверки значимости регрессора в парной регрессионной модели
- •7.Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
- •8.Выбор типа математической функции при построении уравнения регрессии
- •9 Выведите формулы вычисления коэффициентов модели парной регрессии
- •10.Выведите формулы вычисления параметров модели парной регрессии
- •11.Гетероскедастичность - понятие, проявление и меры устранения.
- •12.Гетероскедастичность случайного возмущения. Причины. Последствия. Тест gq.
- •13.Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели
- •21.Индивидуальная и интервальная оценка индивидуального значения зависимой переменной
- •22.Интервальная оценка параметров уравнения парной регрессии
- •23.Классическая парная регрессионная модель. Спецификация модели. Теорема Гаусса – Маркова.
- •24.Ковариация, коэффициент корреляции и индекс детерминации
- •25.Количественные характеристики взаимосвязи пары случайных переменных.
- •26. Косвенный метод наименьших квадратов для оценки параметров структурной формы модели
- •28. Коэффициент корреляции и индекс детерминации в регрессионной модели.
- •29. Линейная модель множественной регрессии
- •30. Метод Монте-Карло, его применение в эконометрике
- •31. Метод наименьших квадратов: алгоритм метода; условия применения. Обобщённый метод наименьших квадратов
- •32. Модели с бинарными (фиктивными) переменными.
- •33. Моделирование тенденции временных рядов (аналитическое выравнивание)
- •34. Мультиколлинеарность факторов – понятие, проявление и меры устранения
- •35. Назначение теста Голдфелда-Квандта, этапы его проведения.
- •36. Нелинейная модель множественной регрессии Кобба-Дугласа. Оценка её коэффициентов.
- •37.Нелинейная регрессия (линеаризация, оценка параметров)
- •38.Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение.
- •39.Основные числовые характеристики вектора остатков в классической множественной регрессионной модели
- •40.Отражение в модели влияния неучтённых факторов и времени.
- •42.Оценка адекватности полученной эконометрической модели (см. 5)
- •43.Оценка коэффициентов модели Самуэльсона-Хикса
- •44.Оценка параметров множественной регрессионной модели методом наименьших квадратов.
- •45. Оценка параметров парной регрессионной модели методом наименьших квадратов.
- •46.Оценка параметров эконометрической модели
- •47.Оценка статистической значимости коэффициентов модели множественной регрессии. (см. 6)
- •48.Подбор объясняющих переменных множественной линейной модели. Алгоритм исключения квазинеизменных переменных
- •49.Подбор объясняющих переменных множественной линейной модели. Метод анализа матрицы коэффициентов корреляции.
- •50.Подбор переменных в модели множественной регрессии на основе метода оценки информационной ёмкости.
- •51.Понятие гомоскедастичности и гетероскедастичности случайных возмущений, их графическая интерпретация.
- •52.Порядок оценивания линейной модели множественной регрессии методом наименьших квадратов (мнк) в Excel
- •53.Последствия гетероскедастичности. Тест Голдфелда-Квандта.
- •54.Предпосылки метода наименьших квадратов
- •55.Применение обобщенного метода наименьших квадратов (омнк) для случая гетероскедастичности остатков.
- •56.Применение теста Стьюдента в процедуре подбора переменных в модели множественной регрессии.
- •57.Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных.
- •58 Принципы спецификации эконометрических моделей и их формы
- •59.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности.
- •60.Проверка качества эконометрической модели См.5
- •61.Прогнозирование экономических переменных. Проверка адекватности модели. См.5
- •62 Простейшие модели временных рядов. Их свойства
- •63.Регрессионные модели с фиктивными переменными.
- •64.Роль вектора и матрицы корреляции множественной линейной модели при подборе объясняющих переменных.
- •65.Свойства дисперсии случайной переменной
- •66.Случайные переменные и их характеристики.
- •67.Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор формы уравнения множественной регрессии.
- •68 Составление спецификации модели временного ряда
- •69.Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам
- •70 Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений
- •71.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
- •72.Статистические свойства оценок параметров парной регрессионной модели.
- •73.Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения.
- •74.Суть метода наименьших квадратов. Его графическое пояснение
- •75.Схема Гаусса – Маркова.
- •76.Схема построения эконометрической модели.
- •77.Теорема Гаусса – Маркова.
- •78.Тест Дарбина – Уотсона, последовательность его выполнения.
- •79.Тест Стьюдента.
- •80. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
- •81. Устранение автокорреляции в парной регрессии. (см. 4)
- •82. Функция регрессии как оптимальный прогноз.
- •83. Цели и задачи эконометрики. Этапы процесса эконометрического моделирования. Классификация эконометрических моделей.
- •84. Эконометрика, её задача и метод.
- •85. Эконометрическая инвестиционная модель Самуэльсона-Хикса.
- •87. Этапы исследования зависимостей между экономическими явлениями при помощи эконометрической модели. Принципы спецификации модели. Формы эконометрических моделей.
- •88. Этапы построения эконометрических моделей
12.Гетероскедастичность случайного возмущения. Причины. Последствия. Тест gq.
Вторым условием Гаусса-Маркова для классической регрессионной модели является независимость дисперсии возмущения от номера (момента) наблюдений (гомоскедастичность – одинаковый разброс). Нарушение этого условия принято называть гетероскедастичностью (неодинаковый разброс).
При наличии гетероскедастичности количественные характеристики вектора возмущений равны:

Причины:
-
Неоднородность исследуемых объектов (например, при анализе зависимости спроса от дохода потребителя выясняется, что чем больше доход, тем больше индивидуальное значение спроса колеблется относительно ожидаемого значения);
-
Характер наблюдений (например, данные временного ряда).
Последствия:
-
При наличии гетероскедастичности МНК обеспечивает несмещенные оценки параметров, но оценка дисперсии возмущений – смещенная, т.е.
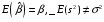
И это приводит к неадекватным оценкам:
-
Автоковариационной матрицы оценок параметров
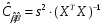
-
Границ доверительных интервалов параметров модели и значений зависимой переменно,
Т.е. последствия такие же, как и от автокорреляции.
Тест GQ.
Предпосылки теста:
1)пропорциональность дисперсии случайного возмущения величине некоторого регрессора Xj
2)случайное возмущение распределено нормально и не подвержено автокорреляции
Алгоритм теста:
-
Упорядочить выборочные данные по величине регрессора Xtj, t=1,…,n, относительно которого есть подозрение на гетероскедастичность (или по сумме модулей регрессоров)
-
По первым и последним n’ данным выборки оцениваются две частные регресии и векторы остатков e1 и e2 соответственно
k+1< n’≈ n/3, k+1 – число параметров модели.
-
По остаткам частных регрессий вычисляются суммы квадратов остатков:
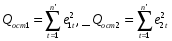
-
вычисляются статистики, имеющие F-распределение:
GQ =Qост1/Qост2, GQ-1=Qост2/Qост1
-
по таблице распределения с двумя параметрами v1 = v2 = n’- k – 1 – число степеней свободы, для уровня значимости α определяется Fкр
-
гипотеза об отсутствии гетероскедастичности принимается, если справедливы оба неравенства GQ ≤ Fkp, GQ-1≤ Fkp, в противном случае делается вывод о гетероскедастичности случайных возмущений.
13.Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели
Выполним оценку
структурных параметров уравнения
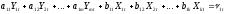 системы
системы
 ДМНК. Запишем уравнения наблюдений, с
учетом условия нормализации, в следующем
виде:
ДМНК. Запишем уравнения наблюдений, с
учетом условия нормализации, в следующем
виде:
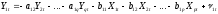 ,
(10.31)
,
(10.31)
t=1,...,n, q – число эндогенных переменных, включенных в первое уравнение, p – число предопределенных переменных первого уравнения.
Введем обозначения:
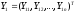 - вектор наблюдений
эндогенной переменной, для которой
выполняется условие нормализации
- вектор наблюдений
эндогенной переменной, для которой
выполняется условие нормализации
 - матрица наблюдений
остальных эндогенных переменных,
включенных в первое уравнение
- матрица наблюдений
остальных эндогенных переменных,
включенных в первое уравнение
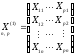 - матрица наблюдений
предопределенных переменных, включенных
в первое уравнение
- матрица наблюдений
предопределенных переменных, включенных
в первое уравнение
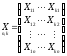 -
матрица наблюдений предопределенных
переменных, включенных в систему
-
матрица наблюдений предопределенных
переменных, включенных в систему
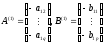 - структурные
параметры уравнения
- структурные
параметры уравнения
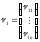 - вектор случайных
возмущений первого уравнения, n
– объем выборки, k
– число предопределенных переменных
в системе.
- вектор случайных
возмущений первого уравнения, n
– объем выборки, k
– число предопределенных переменных
в системе.
Перепишем уравнение (10.31) в новых обозначениях:
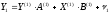 (10.32)
(10.32)
Спецификацию (10.32) можно представить в стандартном виде спецификации множественной регрессионной модели:
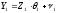 ,
(10.33) где
,
(10.33) где
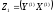 - блочная матрица,
- блочная матрица,
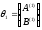 - блочный столбец.
- блочный столбец.
Так как элементы
матрицы
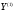 коррелированы с элементами вектора
коррелированы с элементами вектора
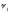 ,
непосредственное применение МНК к
структурной модели приведет к смещенным
и несостоятельным оценкам. Поэтому в
ДМНК поступают следующим образом:
,
непосредственное применение МНК к
структурной модели приведет к смещенным
и несостоятельным оценкам. Поэтому в
ДМНК поступают следующим образом:
Первый шаг:
1. Проводится
регрессия каждого столбца матрицы
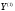 спецификации (10.32)
на все предопределенные переменные
модели, т.е. рассматривается регрессия
спецификации (10.32)
на все предопределенные переменные
модели, т.е. рассматривается регрессия
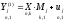 ,
j=1,...,q-1,
где
,
j=1,...,q-1,
где
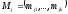 - вектор столбец приведенных параметров
k
x
1 (j-я
строка матрицы коэффициентов приведенной
формы).
- вектор столбец приведенных параметров
k
x
1 (j-я
строка матрицы коэффициентов приведенной
формы).
МНК-оценки вектора
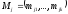 определяются по формуле:
определяются по формуле:
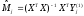 .
.
2. По оцененной модели вычисляется оценка:
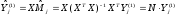 ,
j=1,...,q-1,
и формируется матрица оценок
,
j=1,...,q-1,
и формируется матрица оценок
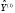 .
.
Второй шаг
Строятся МНК-оценки
структурных параметров
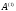 и
и
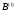 в регрессии:
в регрессии:
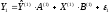 (10.36)
(10.36)
Запишем (10.36) по аналогии с (10.33):
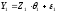 ,
(10.37) где
,
(10.37) где
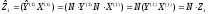 .
(10.38)
.
(10.38)
МНК-оценка параметров регрессионной модели (10.37) имеет вид:
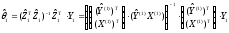 ,
или
,
или
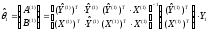 .
(10.39)
.
(10.39)
На основании (10.38) вектор оценок параметров спецификации (10.37) можно представить следующим образом:
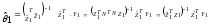 ,
(10.40)
,
(10.40)
с учетом свойства
идемпотентности матрицы N.
Формула (10.40) совпадает с выражением для
оценки параметров (4.22) методом
инструментальных переменных. В качестве
инструмента для стохастических
регрессоров Z
здесь используются их оценки
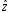 .
.
Автоковариационная
матрица оценок структурных параметров
первого уровня определяется выражением: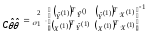 ,
,
Где
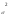 -
дисперсия возмущения первого уровня.
-
дисперсия возмущения первого уровня.
Если для уравнения выполнено ранговое условие идентификации и порядковое условие со знаком равенства (точная идентификация), то оценка ДМНК совпадает с оценкой КМНК. В большинстве экономических компьютерных пакетов для оценки одновременных уравнений реализован двухшаговый МНК.
17.Докажите, что F y, ŷ = t2
Статистика F,
как легко проверить совпадает с квадратом
t-статистики для параметра
b (примечание: в учебнике
написано b, хотя
здесь Невежин требует y.
Eсли попадется,
лучше у него уточнить, но вообще логично,
что параметр – это именно b,
а не y. Если нет,
замените везде b
на y)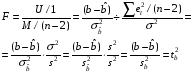
18.Докажите, что ry, ŷ =√R2
Покажем связь
между y и ŷ, и коэффициентом
детерминации R2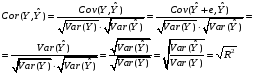
Где учтено, что