68 Составление спецификации модели временного ряда

Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.

Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент. Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение -мультипликативные модели временного ряда. Аддитивная модель имеет вид: Y = Т + S + Е; мультипликативная модель: Y=T* S • Е, где Т- тренд, S- сезонная составляющая, Е – случайная составляющая .

Построение модели включает следующие шаги:

1. выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты S;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (Т + Е) или в мульти­пликативной (Т * Е) модели;

4) аналитическое выравнивание уровней

(Т + Е) или (Т * Е) и расчет значений Т с использованием полученного уравнения тренда;

5) расчет полученных по модели значений

(T + S) или (Т * S);

6) расчет абсолютных и/или относительных ошибок.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда.

Параметры трендов определяются обычным МНК, в качестве не­зависимой переменной выступает время t = 1, 2, ..., п, а в качестве зависимой переменной - фактические уровни временного ряда у_t.

Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации R².

69.Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам

В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование.

Логарифмические модели. Степенные зависимости между переменными широко распространены в практике эконометрического моделирования социально-экономических процессов. Рассмотрим уравнение парной регрессии вида

Y = AX^b где А и b— параметры модели.

Линеаризуем:

прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + b*ln(X) = a+ b*ln(X), где а= ln(A) (*)

Спецификация, соответствующая (*) называется двойной логарифмической моделью:

ln(Y)= a+ b*ln(X)+u,

поскольку и эндогенная переменная, и регрессор используются в логарифмической форме.

Введем обозначения: Y*=ln(Y), X*=ln(X)

Y*=a+b*X+u

Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК.

В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразо­ванным уравнениям. Если в линейной модели и моделях, нели­нейных по переменным, при оценке параметров исходят из кри­терия min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным дан­ным результативного признака, а к их преобразованным величи­нам, т. е.ln y, 1/y. Так, в степенной функции МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на миними­зации суммы квадратов отклонений в логарифмах. Соответственно если в линейных моделях то в моделях, нелинейных по оцениваемым параметрам, . Вследствие этого оценка параметров оказываются несколько смещенной.

Пусть получена МНК-оценка моделиY*=a+b*X+u:

y*=ā + bx+u

(Sā) (Sb) (Su)

Коэффициенты исходной модели и их стандартные ошибки вычисляются с учетом замены по формулам:

А^=exp(ā)

SĀ= А^*Sā

Se, Sb̄, b̄ - такие же

Нелинейный МНК:

В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК).

Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам

наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном

МНК, минимизируется сумма квадратов отклонений:

F=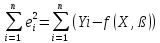² (**)

Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда.

Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn)