47.Оценка статистической значимости коэффициентов модели множественной регрессии. (см. 6)

Вектор-столбец оценок параметров модели по МНК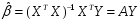. Вектор оценок параметров модели – случайный вектор, его основными количественными характеристиками являются: вектор матожиданий и матрица автоковариаций. Вектор матожиданий:

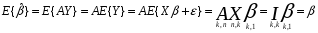
Т.о., МНК-оценки параметров множественной регрессии – несмещенные. Построим матрицу автоковариаций:

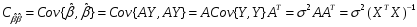Т.к. .

Доказательство эффективности несмещенных оценок 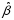выполняется путем сравнения их дисперсий 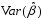с дисперсиями 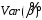вектора линейных несмещенных оценок 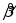, определяемого выражением: 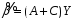, где С-произвольная (к*n)-матрица. Тогда в силу несмещенности оценки 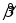и равенства ,

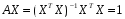Можно записать:

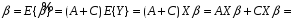
. Откуда следует: СХ=0. Определим автоковариационную матрицу вектора оценок

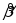
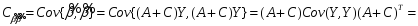
, т.к.

;

.

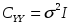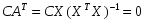
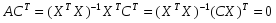Диагональные элементы автоковариационных матриц оценок параметров – их дисперсии. Диагональные элементы матрицы СС^T неотрицательны, поэтому 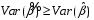, т.е. оценка МНК является эффективной, имея минимальную дисперсию по сравнению с любыми несмещенными оценками неизвестного параметра в классе линейных процедур.

48.Подбор объясняющих переменных множественной линейной модели. Алгоритм исключения квазинеизменных переменных

Предварительным условием присвоения различным величинам статуса объясняющих переменных считается достаточно высокая вариабельность. В качестве меры вариабельности используется коэффициент вариации: 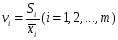где 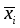-среднее арифметическое 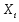. Кроме того, 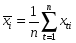, тогда как S_i – стандартное отклонение переменной :

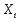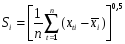
Задается критическое значение коэффициента вариации v*. Переменные удовлетворяющие неравенству 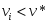признаются квазинеизменными и исключаются из множества потенциальных объясняющих переменных. Эти переменные не несут значимой информации.

49.Подбор объясняющих переменных множественной линейной модели. Метод анализа матрицы коэффициентов корреляции.

Идея этого метода сводится к выбору таких объясняющих переменных, которые сильно коррелируют с объясняемой переменной и одновременно слабо коррелируют между собой. В качестве исходных данных выбирается вектор R₀ (вектор коэффициентов корреляции между объясняемой переменной и всеми объясняющими переменными) и матрица R (коэффициентов корреляции между объясняющими переменными):

R₀= r1 R = 1 r₁₂ … r_1m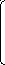

r2 r₂₁ 1 … r_2m

r_m r_m1 r_m2 … 1

Для заданного уровня значимости 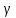и для (n-2) степеней свободы рассчитывается так называемое критическое значение коэффициента корреляции:

r*= 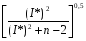где 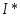- значение t-распределения Стьюдента для заданного 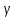и для (n-2) степеней свободы. Критическое значение коэффициентов корреляции также может априорно задаваться аналитиком. Этапы процедуры отбора объясняющих переменных:

1.из множества потенциальных объясняющих переменных исключаются все элементы, которые удовлетворяют неравенству: 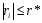, т.к. они несущественно коррелируют с объясняемой переменной.

2.Из оставшихся переменных объясняющей признается такая переменная x_h для которой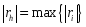 , т.к. x_h является носителем небольшого количества информации об объясняемой переменной.

3.Из множества потенциальных объясняющих переменных исключаются все элементы, которые удовлетворяют неравенству 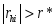, тк эти переменные слишком сильно коррелируют с объясняющей переменной x_h и следовательно только воспроизводят представляемую ею информацию.

Этапы проводятся до момента опустошения множества потенциальных объясняющих переменных.