Электрические нагрузки сельскохозяйственных потребителей

Цель работы

Изучение основ статистического метода определения расчетных электрических нагрузок линий в системах электроснабжения.

Краткие теоретические сведения

По линиям систем электроснабжения питается большое количество электроприемников (жилые дома, больницы, школы, магазины, производственные потребители – животноводческие фермы, зерноочистительные пункты, молокозаводы, консервные заводы и т.д.), режим работы каждого из которых подвержен влиянию значительного количества случайных факторов. Применение аппарата теории вероятностей и математической статистики при исследовании электрических нагрузок позволяет учесть интегральное влияние случайных факторов на величину нагрузки. При этом нагрузка представляется как случайный процесс.Основой для получения числовых характеристик случайного процесса изменения нагрузки - являются случайные графики нагрузки. Графиком нагрузки называется зависимость активной Р, реактивной Q, полной S мощности от времени. Он может быть суточным, годовым, по продолжительности. Суточный график – изменение максимальной получасовой нагрузки в течение суток, годовой – по месяцам года. График нагрузки по продолжительности – это изменение минимальной нагрузки соответствующей рассматриваемому периоду времени от этого времени. При большом числе наблюдений простая статистическая совокупность оказывается неудобной, становится слишком громоздкой и мало наглядной. Для придания ей большей компактности и наглядности статистический материал должен быть подвергнут дополнительной обработке. Результаты наблюдений над непрерывной случайной величиной x оформляются в виде простой статистической совокупности.

Разделив весь диапазон наблюденных значений n на интервалы или разряды, подсчитывается количество значений m_i, приходящихся на каждый i-й разряд. Это число делится на общее число наблюдений и находится частота, соответствующая данному разряду:

.

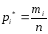Сумма частот всех разрядов должна быть равна единице.

Таблица, в которой разряды приведены в порядке их расположения вдоль оси абсцисс и соответствующих частот, называется статистическим рядом или вариационным рядом :

Ii	xi;x2	x2;x3	…	xi;xi+1	…	xk;xk+1
Pi*	P1*	P2*	…	Pi*	…	Pk*

Значения случайной величины, находящиеся в точности на границе двух разрядов, условно можно считать принадлежащим в равной мере к обоим разрядам и прибавлять к числам m_i того и другого разряда по 0,5.

Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим, но и не слишком малым. Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка 7 - 15. Чем богаче и однороднее статистический материал, тем большее число разрядов можно выбирать при составлении статистического ряда. Длины разрядов могут быть как одинаковыми, так и различными. При оформлении данных о случайных величинах, распределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие, чем в области малой плотности.Упорядоченный статистический ряд в порядке возрастания и весь диапазон их изменения подразделяют на несколько интервалов. Количество интервалов r в зависимости от количества данных в выборке (от количества опытов n ) равно:

n .......... 20 30 50 100 500 1000 10000

r .......... 6 7 8 10 13 15 20

Длина интервала

,

где t₁ и t_n - соответственно наименьшее и наибольшее значение случайной величины в упорядоченном вариационном ряду.

Для значения мощности

,

где Р_мах и Р_мин - соответственно наименьшее и наибольшее значение мощности в упорядоченном вариационном ряду. Значение t обычно округляют до ближайшего числа, имеющего одну- две значащие цифры. Статистический ряд, оформленный графически, называется гистограммой. При построении гистограммы по оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. При равных по длине разрядах высоты прямоугольников пропорциональны соответствующим частотам.

Гистограмма распределения вероятности появления случайной величины представляется в виде гистограммы рис.1.

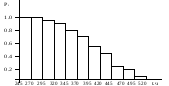
Рис. 1. Гистограмма вероятности появления случайной величины

Из способа построения гистограммы следует, что полная площадь ее равна единице. При увеличении числа опытов можно выбирать все более и более мелкие разряды. Гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Эта кривая представляет собой график плотности распределения величины x.

В результате статической обработки графиков определяются:

1. математическое ожидание мощности (тока, напряжения) нагрузки, являющейся средней величиной мощности нагрузки на некотором интервале времени.

(1)

где n – число реализации графика мощности нагрузки;

Р_ti – вероятность i-той реализации нагрузки.

2. Дисперсия мощности (тока, напряжения) нагрузки:

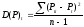(2)

или его среднеквадратическое отклонение (от средней величины):

σ_t(I) = (D (P)_t)^-0.5 (3)

Расчетные нагрузки определяются в часы максимума нагрузок, в течение которых изменение нагрузок является практически стационарным и на этом интервале целесообразно его заменить эквивалентной случайной величиной.

При определении расчетных нагрузок электрических сетей с помощью коэффициентов одновременности k_о используются формулы:

Р_Д = k_о· Σ Р_Дi ; (6)

P_B = k_о· Σ Р_Вi , (7)

где Р_i – суммируемые мощности отдельных потребителей дневного и вечернего максимумов соответственно;

k_о – коэффициент одновременности – отношение расчетной нагрузки группы электроприемников к сумме их максимальных нагрузок.