8. Волны
8.1 Распространение волн в упругой среде.
Если в каком либо месте упругой среды (твёрдой, жидкой, газообразной) поместить источник колебаний, то из-за взаимодействия между частицами колебание будет распространяться в среде от частицы к частице с некоторой скоростью. Процесс распространения колебаний в среде или пространстве называют волной.
Частицы среды не вовлекаются в поступательное движение, они лишь колеблятся у положений равновесия.
Различают продольные и поперечные волны. Первые возникают в среде, обладающей сопротивлением сдвигу, поэтому в газах и внутри жидкостей возникают только продольные волны. На поверхности жидкости –поперечные (колебания поплавка).
Распространняясь
от источника колебаний, волновой процесс
охватывает все новые и новые области
пространства. Геометрическое место
точек, до которых доходят колебания к
моменту времени
,
называется фронтом волны или волновым
фронтом. Это поверхность, которая
отделяет часть среды, которая вовлечена
в волновой процесс, от той ее части, до
которой колебания еще не достигли.
Геометрическое место точек, колеблящихся в одинаковой фазе называют волновой поверхностъю. Эту поверхность можно провести через любую точку пространнства, в которой есть волновой процесс. Таким образом, волновых поверхностей множество, а волновой фронт один.Волновая поверхность неподвижна, фронт перемещается.
В постейшем случае волновая поверхность и фронт имеют форму сферы и плоскости. Волна тогда называется сферической или плоской. В сферической волне волновые поверхности-концентрические сферы,
в плоской - параллельные плоскости.
Рассмотрим
случай, когда плоская волна распространнняется
вдоль оси
.
Все
точки с определенной координатой
имеют одинаковые фазы (при разных
и
).
На рис
-смещение
точек с разными
в некоторый момент времени
,
т.е.
при
=
const.
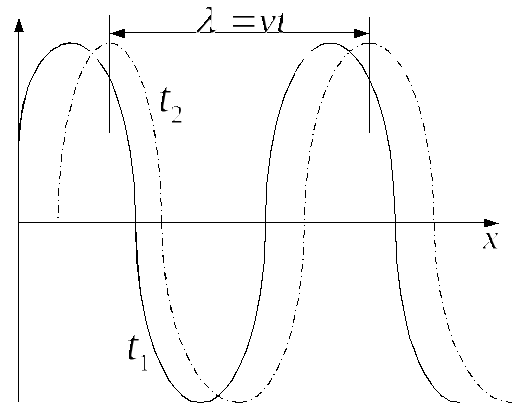
Рис.8,1
С
течением времени кривая перемещается
вдоль оси
.Такой
график можно строить как для поперечних
так и для продольных волн. При этом
-длина
волны,
,
где
-скорость
распространения волны.
8.2 Уравнение плоской и сферической волн.
Уравнение
волны выражает зависимость смещения
колеблющейся частицы от ее кординат
,
,
и времени
:
.
Эта
функция должна быть периодической
относительно времени, т.к. она описывает
колебания частицы с координатами
,
,
,
и периодическая относительно координат,
т.к. точки среды, отстоящие друг от друга
на
длину волны
,
колеблются одинаковым образом.
Найдём
вид функции
для плоской волны, для гармонических
колебаний, распространяющихся вдоль
оси
.Волновые
поверхности здесь перпендикулярны оси
, и смещение
будет зависить только от
и
.
Уравнение колебаний точек в плоскости
имеет вид:
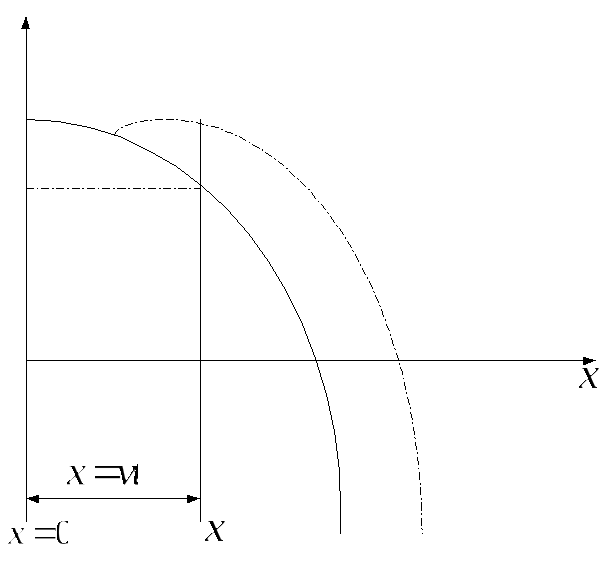
Рис.8,2
Найдем
уравнение колебания для точки с
произвольным
,
дойти до которой волне требуется время
.
Значит колебания частиц в плоскости
будут отставать во времени на
от колебаний в плоскости
:
*
- уравнение плоской волны, распространяющейся
в направлении оси
со
скоростъю
,
величина
- фаза волны, начальная фаза
определяется
выбором начала отсчёта
и
,
для одной волны обычно принимают
.
Зафиксировав
определенное значение фазы
,
можно найти связь между коорлинатой и
временем для которых
,
а величина
при этом даёт значение скорости, с
которой перемещяется это значение фазы
т.е., можно проследить движение определенной
фазы волны. Взяв дифференциал от
,
получим:
и
.
Таким образом, скорость распространения волны в уравнении (*) есть скорость перемещения фазы, поэтому ее называют фазовой скоростъю волны.
Уравнение
(*) описывает волны, распространяющиеся
в сторону возрастания
.
Волна обратная имеет вид:
.
Уравнению
волны можно придать более симметричный
вид относительно
и
,
если ввести понятие волнового числа
и
волнового вектора
,
где
- нормаль к волновому фронту. Умножив
числитель и знаменатель
на
,
получим:
.
Тогда,
и уравнение волны:
.
Теперь
найдем уравнение сферической волны для
точечного источника. Все точки сферической
волновой поверхности волны в однородной
и изотропной среде будут колебаться с
одинаковой фазой. Если фаза источника
,
то фаза точек волновой поверхности
радиуса
равна
.
Амплитуда колебаний сферической волны
будет убывающей, даже если нет затухания
и убывает по закону
.
Тогда уравнение сферической волны:
.
Для поглощающей среды появится
дополнительный множитель
.
Уравнение
плоской волны, распространяющейся в
произвольном направлении
имеет вид:
.