7.6 Автоколебания
При затухающих колебаниях энергия системы постепенно уменьшается и колебания прекращаются. Для того, чтобы их сделать незатухающими, необходимо пополнять энергию системы извне в определенные моменты времени в такт колебаниям, иначе можно уменьшить амплитуду колебаний. Т.е.необходимо сделать систему такой, чтобы она сама управляла внешним воздействием, обеспечивая синхронность внешних толчков колебаниям системы (примером могут быть качели).Такая система называется автоколебательной, а колебания автоколебаниями. Пример-часы. Маятник находится на одной оси с анкером с палеттами.
7.7 Вынужденные колебания
Если
колебательная система, кроме сил
сопротивления, подвергается действию
внешней периодической силы, изменяющейся
по гармоническому закону
,
то уравнение 2-го закона Ньютона:
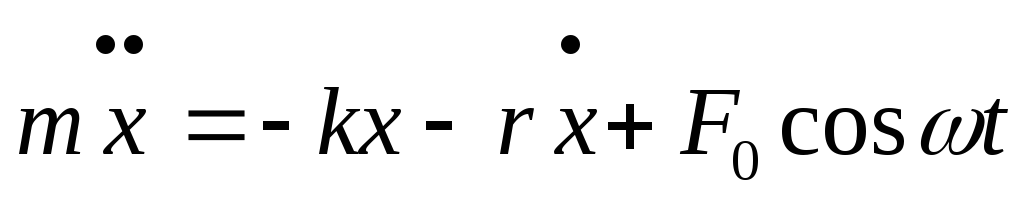
или
с обозначениями
,
,
()-
уравнение вынужденых колебаний. Здесь
-частота
внешней силы,
-собственная
частота системы.
Это неоднородное дифференциальное уравнение, решение которого состоит из суммы решений соответствуещего однородного уравнения (без правой части) и частного решения неоднородного уравнения.
Решение
однородного уравнения известно:
,
это затухающие колебания с частотой
,
,
-произвольные постоянные.
Частное
решение уравнения ()
имеет форму:
или, раскрывая его:
()
где
-амплитуда
колебаний, а
- фаза.
Это
решение не содержит произвольных
постоянных. Значение
представляет собой отставание по фазе
вынужденного колебания от вынуждающей
силы F.
Сумма
решений дает обшее решение уравнения
(*), описывающего вынужденные
колебания. Первое слагаемое играет
заметую роль только в начальной стадии
процесса, т.е.,
при установлении колебаний. Со временем
амплитуда этого слагаемого экспоненциально
падает и
им можно пренебречь, сохраняя второе
слагаемое. Таким образом, функция (**)
описывает установившееся колебание,которое
происходит с частотой
,
т.е.,
равной частоте внешней силы.Их амплиткда
пропорциональна амплитуде вынуждающей
силы
,
и для данной системы (с параметрами
,
)
зависит от частоты
внешней силы. Отставание по фазе также
зависит от
.
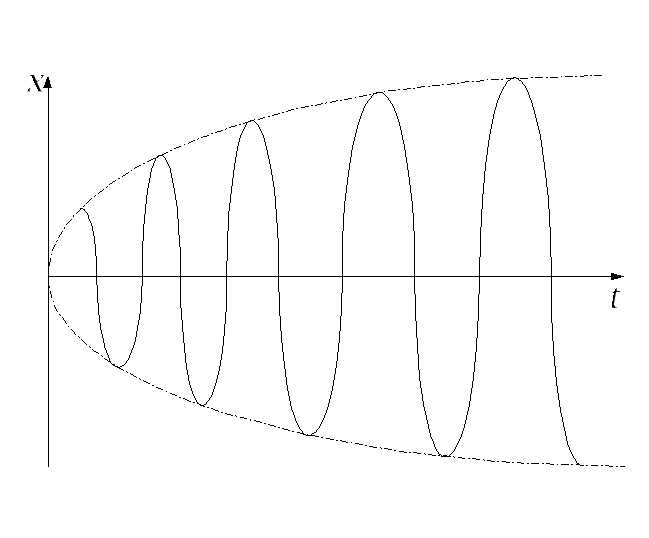
Рис.7,9
7.8 Резонанс
Кривая
зависимости амплитуды вынужденых
колебаний от
приводит к тому, что при некоторой
определенной для данной системы частоте
амплитуда колебаний достигает
максимального значения , а затем с
повышением частоты - уменьшается. Это
явление называется резонансом, а
соответствующая
-резонансной частотой.
Резонансную
частоту можно найти из условия максимума
амплитуды колебаний
,
т.е. нужно взять производную функции и
приравнять ее нулю.
При
этом имеется три решения :
(тривиальное) и
;
,
не подходит: т.к., это означает отсутствие
колебаний; отрицательная частота не
имеет физического смысла.
Значит,
остается
,
при этом резонансная амплитуда
При
(отсутствие сопротивления)
,
а резонансная частота совпадала бы с
частотой собственных колебаний
,
при этом
,
т.е., сдвиг фаз отсутствует.
Зависимость
для разных коэффициентов затухания
имеет
вид кривих с максимумами.
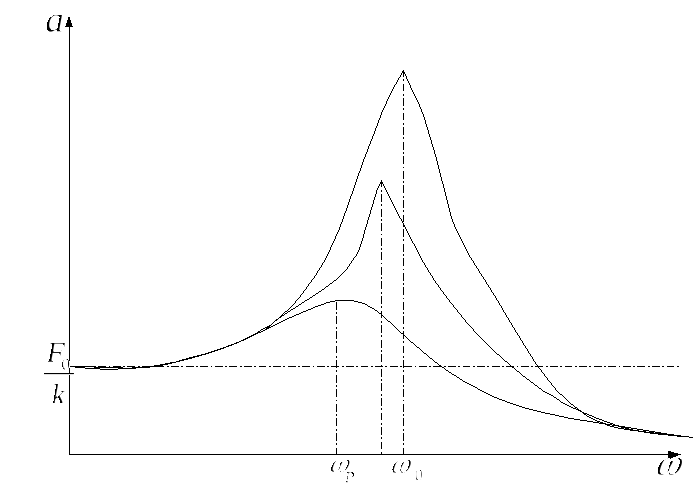
Рис.7,10
Чем
меньше
-
тем острее резонанс, тем выше и правее
лежит максимум. При большом
колебания прекращаются и не имеет смысла
говорить о резонансе.
При
все кривые приходят к предельному
значению амплитуды
-смещение
от положения равновесия под действием
силы
.
При
амплитуда
,
т.к. система неуспевает
следить
за частотой
.
С явленим резонанса необходимо считаться при конструировании машин и сооружений, частота собственных колебаний не должна быть близкой к частоте внешних сил.