34. В тетрадке

35. Чтобы построить график функции, рекомендуется исследовать ее по следующей схеме:

1) найти область определения функции, промежутки непрерывности и точки разрыва;

2) найти асимптоты графика функции;

3) проверить симметрию графика, периодичность;

4) найти интервалы монотонности, экстремумы;

5) найти интервалы выпуклости, вогнутости, точки перегиба;

6) найти точки пересечения с осями координат;

7)  провести в случае необходимости исследование на концах области определения;

8) построить график функции.

36. Нахождение наименьшего и наибольшего значений дифференцируемой функции на замкнутом интервале.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции  на отрезке  :

1. найти ;

2. найти точки, в которых  или 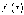 не существует, и отобрать из них те, что лежат внутри отрезка ;

3. вычислить значения функции  в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции  на отрезке  , которые можно обозначить так: .

Если поставлена задача найти  для непрерывной на  функции  , то она решается по тому же правилу, что соответствующая задача для отрезка  .

37. Определение функции нескольких переменных как функции переменной точки.

Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

z = f(x, y)

 38. Определение и геометрический смысл частных производных функции нескольких переменных.

Определение. Частной производной функции  по переменной   в точке  называют предел

Частная производная обозначается одним из символов.

Аналогично определяется частная производная по y:

                                 .

Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.

   4. Геометрическая интерпретация частных

               производных функции двух переменных

 

Пусть уравнение z=f(x,y) –это уравнение поверхности. Проведем плоскость x=const.  L- линия пересечения поверхности с плоскостью x=const. При данном x на плоскости ХОУ возьмем точку М. На поверхности z=f(x,y) ей соответствует точка Р(x,y,z). Дадим переменному y приращение Тогда функция z получит приращение  Отношение  равно тангенсу угла, образованного секущей RР с положительным направлением оси ОУ,

Итак, частная производная  численно равна тангенсу угла

наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.

 Аналогично, частная производная  численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y)плоскостью x=const.

39.

40.

41. Теорема Если смешанные частные производные, отличающиеся лишь порядком дифференцирования, непрерывны в некоторой точке, то их значения в этой точке равны.

42.

43. Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Пусть функция f(x,y) имеет полные производные вплоть до n-го порядка включительно в некоторой окрестности точки (x₀,y₀). Введём дифференциальный оператор

.

Тогда разложением в ряд Тейлора функции f(x,y) по степеням (x − x₀)^k и (y − y₀)^k в окрестности точки (x₀,y₀) будет

где R_n(x,y) — остаточный член в форме Лагранжа:

В случае функции одной переменной , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе T.

44.

45. Достаточные условия существования локальных экстремумов

• Пусть функция 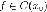 непрерывна в  и существуют конечные или бесконечные односторонние производные . Тогда при условии

x₀ является точкой строгого локального максимума. А если

то x₀ является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x₀

• Пусть функция f непрерывна и дважды дифференцируема в точке x₀. Тогда при условии

 и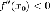 

x₀ является точкой локального максимума. А если

 и 

то x₀ является точкой локального минимума.

Модуль 2.

1. Непустое множество V для элементов которого определенно сложение и умножение на действительные числа называют действительным пространством или линейным пространством.

правила действия с элементами векторных пространств.

1)существ. нейтральный элемент по отношению к операции сложения, этот элемент 0, такой что a+0=а, 0-называется нулевым вектором.

обратный по отношению операции сложения такой что а+(-а)=0. –а – противоположный к а

3)уравнение а+х=в , разрешимо единств. образом ; !:х=в-а, т.е. х=в+(-а)

4)аксиомы ассоциативности и коммуникативности сложения и аксеомы дистрибутивности можно обобщить на любое число слогаемых.

2. Непустое конечное множество Sа1, а2 … аn) элементов векторного пространства V называется линейно зависимым если существуют действительнве числа лямда1, лямда2, лямдаn принадлежащие R одновременно все не равные 0, такие что лямда1*а1 + лямда2*а2 +… +лямдаn*аn=0 (линейная комбинация, линейная зависимость)

3. Непустое множество векторов векторного пространства называется линейным подпространством, если: для любых векторов ;для всех .

4. Линейная оболочка подмножества X линейного пространства L — пересечение всех подпространств L, содержащих X.

Линейная оболочка является подпространством L.

Линейная оболочка также называется подпространством, порожденным X. Говорят также, что линейная оболочка натянута на множество X.

Линейная оболочка состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из X. В частности, если X — конечное множество, то состоит из всех линейных комбинаций элементов X.

Если X — линейно независимое множество, то оно является базисом и тем самым определяет его размерность.

5. Число базесных векторов показывается размерностью векторного пространства. Если векторов 2 то размерность =2, если 3 то 3.

Векторное пространство содержашее нулевой вектор имеет размерность 0. Если векторное пространство не порождается конечной системой базеса то он называется бесконечно мерным

7. Нормой (длиной) вектора x О E называется число, равное

√(x, x)

и обозначаемое || x || .

Из аксиом скалярного произведения следуют свойства нормы:

|| x || >0 "x ≠ θ ; || x || = 0 ЬЮ x = θ . || x + y || ≤ || x || + || y || .

Вектор, норма которого равна единице, называется единичным (нормированным) вектором, или ортом

8. Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица A = (aij) размера при этом преобразовании станет матрицей размерностью .

Две матрицы равны когда они одного размера и все их элементы совпадают.

A = B

Матрица представляет из себя таблицу чисел размером mxn, где первое число m - количество строк, а второе n - количество столбцов. Это нужно запомнить: первое число - строка, второе число - столбец.

12. Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

Метод Жардана –Гауса основан на преобразовании расширенной матрицы к виду при котором r переменных образуют диагональную матрицу с точностью до перестановки строк и столбцов что позволяет сразу найти решение. На каждом шаге выбирается разрешающий элемент аqs неравный 0 если возможно=1, он стоит в q строке, которая называется разрешающей строке и s разрешающем столбце..

Обратная матрица …

/А/

Аt

Aij = (-1)i+j * Mij

A(c волной) = Aij

А-1 = *A(с волной)

14. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю. Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю. Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю. Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей.

17. 1-/А/

2-Аt

3-Aij = (-1)i+j * Mij

4-A(c волной) = Aij

5-А-1 = *A(с волной)

6- проверка А-1 *А =Е

18. Лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

1) сложение операторов по формуле (А + B)х = Ах + Bх

2) умножение оператора на число по формуле (лА).х = л(Ах);

3) умножение операторов по формуле (АВ}х = А(Вх).

24. Пусть ∆=/А/,

∆-определитель главной матрицы системы.

∆i –определитель матрицы полученной из матрицы А путем замены i столбца матрицы А столбцом свободных членов., решение системы линейных упавнений

Хi=

Х1= , Х2=

28. Когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором

Свободный вектор может, следовательно, быть перемещаем в пространстве как угодно параллельно самому себе, причем длина и смысл направления остаются неизменными.

30. Какие векторы называются коллинеарными? Что такое орт вектора? Коллинеарные векторы это векторы, лежащие на одной прямой или на параллельных прямых. Для того чтобы два ненулевых вектора были коллинеарные, необходимо и достаточно, чтобы их координаты были пропорциональны. Нулевой вектор коллинеарен всякому вектору. Единичные векторы (орты) - это векторы, абсолютная величина (модуль) которых равен единице. Этот единичный вектор направлен туда же, куда направлен и сам вектор а, и его модуль равен единице, то есть а_n= 1.

31. Проекции вектора на ось и на вектор. Свойства проекций. Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора. Проекцией вектора b на вектор a, a НЕ = 0, будем называть проекцию вектора b на любую ось, параллельную вектору a и имеющую направление, совпадающее с направлением вектора a. Проекция вектора b на вектор a обозначается П p_ab

32. Дать определение базиса векторов а) на плоскости, б) в пространстве. Описать разложения вектора по базису. Базисом на плоскости называются два неколлинеарных вектора e₁ e₂ на этой плоскости, взятые в определённом порядке. Эти векторы e₁ e₂ называются базисными. Базисом в пространстве называются три некомпланарных вектора e₁, e₂, e₃ , взятые в определённом порядке. Эти векторы e₁, e₂, e₃ называются базисными.

33. Дать понятие ортонормированного базиса и ориентации базиса. Как определяются прямоугольные координаты вектора? Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Аффинная система координат называется прямоугольной, если ее базис ортонормированный. Выбирая стандартные базисы, получаем: прямоугольную систему координат в пространстве — это точка О и три попарно перпендикулярных единичных вектора i, j, k (i- первый базисный вектор, j — второй, а k— третий; тройка векторов i,j, k— правая) . Координаты векторов и точек в прямоугольной системе координат называются прямоугольными координатами. Координатами вектора в прямоугольной системе координат называются коэффициенты в разложении вектора по стандартному базису.

34. Определить действия скалярного, векторного и смешанного произведений векторов, перечислить их свойства и указать их выражения через прямоугольные координаты. Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром. (Масса тела, объем, время и т.д.)1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов a и b aхb=bхa; 2. Для любого числа λ и любых векторов a, b имеем: λ(axb)= (λxa)xb=ax(λxb); 3. Для любых векторов a,b,c выполняется равенство (a+b)xc=axc + bxc; 4. Для любого вектора a выполняется соотношение a²=axa=/a/²; 5. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором. (Перемещение, сила, скорость и т.д.) 1..При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. bxa= -(axb); 2. Векторный квадрат равен нуль-вектору, т.е.axa= 0; 3.Скалярный множитель можно выносить за знак векторного произведения, т.е. kaxb=axkb=k(axb); 4. Для любых трех векторов a,b,c справедливо равенство (a+b)xc=axc + bxc; 5. Необходимое и достаточное условие коллинеарности двух векторов a и b : axb = 0. Смешанным (векторно-скалярным) произведением векторов называется число, определяемое по формуле: abc= (axb)xc=ax(bxc) 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. abc=bca=cab; 2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. bac=abc =cba= -abc; 3.Необходимое и достаточное условие компланарности трех векторов abc= 0; 4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.abc=+-V.

35.

36. Дать определение прямоугольной системы координат на плоскости и в пространстве. Как определяются координаты точки? Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях.

37.

38.

39.

40. Дать определение полярной системы координат на плоскости. Написать формулы связи между полярными и прямоугольными координатами точки. Полярная система координат на плоскости — это совокупность точки O, называемой полюсом, и полупрямой OX, называемой полярной осью.

41. Дать определение цилиндрической и сферической систем координат в пространстве Цилиндрическими координатами точки М называются числа (r, q, h), которые определяют положение точки М в пространстве. Сферическими координатами точки М называются числа (r,j,q), где j - угол между r и нормалью.

42.

43. Сформулировать задачу о взаимном расположении прямых на плоскости и описать способ ее решения. L1:3x-4y+11= 0 и L2:2x-3y+8= 0 Алгоритм решения систем уравнений способом подстановки. Выразить из любого уравнения системы одну переменную через другую; подставить полученное выражение вместо этой переменной в другое уравнение системы решить полученное уравнение с одной переменной; найти соответствующее значение второй переменной.

44.

45. Расстояние от точки до прямой

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

                                                                      (1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

            Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

.Теорема доказана.

Или

Пусть дана какая-нибудь прямая и произвольная точка 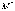; обозначим через d расстояние от точки М* до данной прямой. Отклонением  точки  от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и -d, если данная точка и начало координат расположены по одну сторону от данной прямой. (Для точек, лежащих на самой прямой, =0). Если даны координаты ,  точки  и нормальное уравнение прямой , то отклонение  точки от этой прямой может быть вычислено по формуле

.

Таким образом, чтобы найти отклонение какой-нибудь точки  от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки . Полученное число будет равно искомому отклонению.

Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: .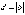

Если дано общее уравнение прямой , то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель , определяемый формулой

.

Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

46. Окружность – множество всех точек плоскости, равноудаленных от данной точки на плоскости.

Выведем уравнение окружности.

Пусть C(a, b) – центр окружности, а R – ее радиус. Возьмем произвольную точку M(x, y) ∈  окр.

Расстояние от центра окружности до точки M находится по известной формуле

Каноническое уравнение окружности. В центре с координатами a и b и радиусом R

Если в этом уравнении раскрыть скобки и выполнить некоторые преобразования, то получим:

Приведение уравнения окружности к каноническому виду:

47. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.       

Каноническое уравнение

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

Свойства

Оптические

Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

Если F₁ и F₂ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой(F₁X) равен углу между этой касательной и прямой (F₂X).

Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

Эволютой эллипса является астроида.

Точки пересечения эллипса с осями являются его вершинами.

Эксцентриситет эллипса равен отношению . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

Эллипс также можно описать как

фигуру, которую можно получить из окружности, применяя аффинное преобразование

ортогональную проекцию окружности на плоскость.

Пересечение плоскости и кругового цилиндра

48. Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами  и , расстояние между ними - через 2с. По определению гиперболы , или .

Канонический вид

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду

,

где большая a и малая b полуоси.

Свойство 10.6. 

Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называютсявершинами гиперболы.

Доказательство

Отрезок AB называется действительной осью гиперболы, его длина равна 2a. Число a называется действительной полуосью гиперболы, число b – мнимой полуосью.

Свойство 10.7. 

Гипербола имеет две взаимно перпендикулярные оси симметрии.

Доказательство

Свойство 10.8. 

Гипербола имеет центр симметрии.

Доказательство

Центр симметрии гиперболы называют центром гиперболы.

Свойство 10.9. 

Гипербола пересекается с прямой y = kx при  в двух точках. Если  то общих точек у прямой и гиперболы нет.

Доказательство

Так как гипербола симметрична относительно осей координат, то достаточно изучить ее форму в первом квадранте координатной плоскости. Из полученных формул 

видно, что при возрастании k от нуля до  (при этом угол наклона прямой к оси Ox возрастает от нуля до некоторого значения) и абциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая y = kx пересекает гиперболу во все более далеких от начала координат точках. Таким образом, гипербола имеет вид, изображенный на рис. 10.9.1, и состоит из двух не связанных между собой частей, называемых ее ветвями.

49. Пара́бола  — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки(называемой фокусом параболы).

 В выбранной системе координат ее уравнение имело вид 

Сделаем поворот системы координат на угол 90°, воспользовавшись формулами поворота 

Запишем уравнение параболы в новой, канонической системе координат: 

Свойство 10.10. 

Парабола имеет ось симметрии.

Доказательство

Ось симметрии называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы в канонической системе координат находится в начале координат.

Свойство 10.11. 

Парабола расположена в полуплоскости x ≥ 0.

Доказательство

При замене системы координат заданная в условии точка A с координатами  будет иметь новые координаты, определяемые из соотношений 

Таким образом, точка A будет иметь в канонической системе координаты  Данную точку  называют фокусом параболы и обозначают буквой F.

Прямая l, задаваемая в старой системе координат уравнением  в новой системе координат будет иметь вид 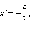 или, опуская штриховку, 

Данная прямая в канонической системе координат называется директрисой параболы. Расстояние от нее до фокуса называется фокальным параметром параболы. Очевидно, он равен p. Эксцентриситет параболы по определению полагают равным единице, то есть ε = k = 1.

Теперь свойство, через которое мы определили параболу, в новых терминах можно сформулировать следующим образом: любая точка параболы равноудалена от ее фокуса и директрисы.

Вид параболы в канонической системе координат и расположение ее директрисы приведены на рис. 10.10.1.

50. Установленное свойство эллипса и гиперболы можно положить в основу общегоопределения этих линий: множество точек, для которых отношение расстояний до фокуса и до соответствующей директрисы является величиной постоянной, равной ε , есть эллипс, если ε<1, есть гипербола, если ε>1.

51. Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “e” или “ε”.

Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.

Связанные определения

Точка F называется фокусом конического сечения.

Прямая d называется директрисой, число e — эксцентриситетом.

Свойства

В зависимости от эксцентриситета, получится:

при e > 1 — гипербола.

при e = 1 — парабола;

при e < 1 — эллипс;

для окружности полагают e = 0.

Эксцентриситет эллипса может быть выражен через отношение большой (a) и малой (b) полуосей:

Для эллипса также может быть выражен через отношение радиусов пери- (r_p) и апоцентров (r_a):

Для эллипса и гиперболы эксцентриситет равен отношению расстояния между фокусами к большей или вещественной оси.

52. Полярное уравнение конических сечений. Примем фокус F конического сечения за полюс полярной системы координат, ось которой направлена перпендикулярно к директрисе f и не пересекает ее. Расстояние от фокуса до директрисы обозначим через m. Очевидно, что полярные координаты r и φ произвольной точки M конического сечения (см. Рис. 1) связаны соотношением

r cos φ + m = d,

где d - расстояние от точки M до директрисы. С другой стороны, согласно определению конического сечения, имеем d = r : ε.

     Следовательно,

     Из этого уравнения находим:

Это и есть полярное уравнение конического сечения. При φ = 90° имеем r = mε. Этот полярный радиус обозначают обычно через p (параметр конического сечения); он равен фокальной полухорде, перпендикулярной к полярной оси.

53. Плоскость задается тремя произвольными точками, не принадлежащими одной прямой. Плоскость в пространстве можно задать:

тремя точками, не лежащими на одной прямой (рис. 5.1, а);

прямой и не принадлежащей ей точкой (рис. 5.1, б);

двумя пересекающимися прямыми (рис. 5.1, в);

двумя параллельными прямыми (рис. 5.1, г);

любой плоской фигурой (рис. 5.1, (3).

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz

Уравнение плоскости, проходящей через три точки

            Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

            Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат.

            Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы  были компланарны.

() = 0

Таким образом,              

Уравнение плоскости, проходящей через три точки:

Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости

            Пусть заданы точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂) и вектор .

Составим уравнение плоскости, проходящей через данные точки М₁ и М₂ и произвольную точку М(х, у, z) параллельно вектору .

Векторы и вектор  должны  быть компланарны, т.е.

() = 0

Уравнение плоскости:

Уравнение плоскости по одной точке и двум векторам,коллинеарным плоскости

Пусть заданы два вектора  и , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы  должны быть компланарны.

            Уравнение плоскости:

                         

 

Уравнение плоскости по точке и вектору нормали

Теорема. Если в пространстве задана точка М₀(х₀, у₀, z₀), то уравнение плоскости, проходящей через точку М₀ перпендикулярно вектору нормали (A,B, C) имеет вид: 

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

            Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор . Т.к. вектор  - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору . Тогда скалярное произведение

×= 0

Таким образом, получаем уравнение плоскости

Теорема доказана.

Уравнение плоскости в отрезках 

            Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)

,

заменив , получим уравнение плоскости в отрезках:

 

            Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

Уравнение плоскости в векторной форме

 где

- радиус- вектор текущей точки М(х, у, z),

 - единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.

 

a, b и g - углы, образованные этим вектором с осями х, у, z.

p – длина этого перпендикуляра.

 

            В координатах это уравнение имеет вид:

xcosa + ycosb + zcosg - p = 0

Расстояние от точки до плоскости

Расстояние от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно:

            

Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

            

  Таким образом, A = 4/13;  B = -3/13;   C = 12/13, воспользуемся формулой:

  A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

54.   Способы задания прямой       Векторно-параметрическое уравнение прямой 

где  - фиксированная точка, лежащая на прямой;  - направляющий вектор.

     В координатах (параметрические уравнения):

     Канонические уравнения прямой 

     Уравнения прямой по двум точкам 

     Прямая как линия пересечения двух плоскостей 

при условии, что не имеют места равенства

     Направляющий вектор такой прямой

где,

55. ???

56. ???

57. ???

58. уравнение эллипсоида;

уравнение мнимого эллипсоида;

уравнение мнимого конуса;

уравнение однополостного гиперболоида;

уравнение двуполостного гиперболоида;

уравнение конуса;

уравнение эллиптического параболоида;

уравнение гиперболического параболоида;

уравнение эллиптического цилиндра;

уравнение мнимого эллиптического цилиндра;

уравнение пары мнимых пересекающихся плоскостей;

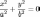
уравнение гиперболического цилиндра;

уравнение пары пересекающихся плоскостей;

уравнение параболического цилиндра;

уравнение пары параллельных плоскостей;

уравнение мнимых пары параллельных плоскостей;

уравнение пары совпадающих плоскостей.