Модуль 1
1. Способы задания множеств. Множество может быть задано следующим образом:
– перечислением всех его элементов по их названиям ( так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);Пример:Множество учеников данного класса определяется их списком в классном журнале, множество всех стран на земном шаре - их списком в классном журнале, множество всех костей в человеческом теле - их списком в учебнике анатомии.
Но этот способ применим только к конечным множествам, но и то не ко всем.
Пример:Свойство "быть квадратом целого числа" задает (бесконечное) множество всех квадратов целых чисел.
Задание множеств их характеристическим свойством иногда приводит к осложнениям. Может случиться, что два различныххарактеристических свойства задают одно и то же множество, т.е всякий элемент,обладающий одним свойством, обладает и другим, и обратно.
Пример:Хотя множество всех рыб в океане конечно, вряд ли его можно задать списком.
- описание в тех случаях, когда множество нельзя задать при помощи списка, его задают путем указания некоторого характеристического свойства.Свойство является характеристическим для некоторого множества, если этому множеству принадлежат в точности те элементы, которые обладают данным свойством.
2.Натуральные числа - числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления), т.е натуральные числа - это естественные числа.
Натуральными числами не являются: отрицательные и нецелые числа.
N={1;5;8}
Множество целых чисел
,
Оно состоит из натуральных чисел (1, 2,
3), чисел вида -n (
)
и числа нуль.
Множество, состоящее из всех целых положительных и отрицательных чисел, нуля и положительных и отрицательных дробей, называется множеством всех рациональных чисел
-
Дать определение равенства множеств с помощью отношения включения.
(определение равенства множеств). Множества А и B равны, если они состоят из одних и тех же элементов, то есть, если из x A следует x B и обратно, из x B следует x A.
Формально равенство двух множеств записывается следующим образом:
(А=В):= x((x A) (x B)),
это означает, что для любого объекта x соотношения x A и x B равносильны.
-
A=A(рефлексивность);
-
Если А=В, то В=А(симметричность);
-
Если А=В и В=С, то А=С(транзитивность).
Отношение включения
множество А содержится
в
множестве В или множество А является подмножеством множества В ( в
этом случае пишут А 
В ), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения: 
А
и А 
А .
4. В тетрадке
5.
Прямым произведением или декартовым
произведением
множеств
и
называется множество всех упорядоченных
пар
таких, что
и
. При этом используют следующее
обозначение:
6.Из каких элементов состоит множество действительных чисел?
Действительные числа, не являющиеся рациональными, называются иррационалъными. Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
N={1; 2; 3; ...; n; ... } — множество натуральных чисел;
Zo={0; 1; 2; ...; n; ... } — множество целых неотрицательных чисел;
Z={0; ±1; ±2; ...; ±n; ...} — множество целых чисел;
Q={m/n: mÎZ,nÎN} — множество рациональных чисел.
R—множество действительных чисел.
Между этими множествами существует соотношение
NÌ ZoÌ ZÌ QÌ R.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 1/2= 0,5 (= 0,500...), 1/3=0,333... — рациональные числа.
7.Числовая прямая - это множество действительных чисел.
Геометрической моделью числовой прямой служит координатная прямая.
8.Абсолю́тная величина́ или мо́дуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом: - если x > 0, то | x | = x; - если x <= 0, то | x | = − x.
Для любых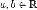 
имеют
место следующие соотношения:
-
(см. Функция
sgn(x)). -
-
.
Как для вещественных, так
и для комплексных 
имеют
место соотношения:
-
,
причём | a |
= 0 тогда и только тогда, когда 
. -
| − a | = | a | .
-
. -
(неравенство
треугольника). -
. -
. -
. -
,
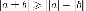если 
существует.
9. Промежуток, или более точно, промежуток числовой прямой — множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними.
Окрестностью
точки 
называется
всякое открытое множество, содержащее
эту точку. И, как следует из определения
открытых множеств топологии τ, всякая
окрестность точки a включает
один из интервалов указанного вида,
содержащий a.
10.Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённойпроцедуры выбранных из генеральной совокупности для участия в исследовании.
Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.
11.Прямое или декартовое произведение двух множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств.
14. Бином - иначе двучлен.
|
При n=1 |
(a + b)1=a+b, |
|
При n=2 |
(a + b)2=a2+2ab+b2, |
|
При n=3 |
(a + b)3=a3+3a2b+3ab2+b3, |
|
При n=4 |
(a + b)4=a4+4a3b+6a2b2+4ab3+b4. |
Свойство коэффициэнтов бинома Ньютона
-
Коэффициенты членов, равноудаленных от концов разложения, одинаковы.
-
Сумма коэффициентов разложения (a + b)n равна 2n. Для доказательства этого свойства достаточно рассмотреть бином, у которого a = b = 1. С одной стороны бином (1 + 1)n =2n. C другой стороны бином равен сумме всех биномиальных коэффициентов.
-
Сумма коэффициентов членов, стоящих на нечетных местах, равна сумме коэффициентов членов, стоящих на четных местах. Каждая из них составляет 2n-1.Чтобы убедиться в этом достаточно рассмотреть бином, у которого a = 1, b = -1.
Формула бинома Ньютона позволяет доказать важную зависимость между биномиальными коэффициентами : Cnm+1 = Cnm + Cnm+1.
15.
16.
Разбие́ниемно́жества —
это представление его в
виде объединения произвольного
количества попарно непересекающихся подмножеств.
Семейство непустых множеств
,
где A — некоторое множество индексов
(конечное или бесконечное), называется
разбиением X, если:
1.
для любых
,
таких что
;
2.
17. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.
18.Свойство дифференцируемости функции. Понятие дифференциала.
Линейную
функцию 
называют дифференциалом
функции f в
точке 
и
обозначают df.
Для функции x производная
в каждой точке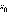 
равна 1,
то есть 
Поэтому
пишут:
|
Приближенное значение
функции вблизи точки 
равно
сумме ее значения в этой точке и
дифференциала в этой же точке. Это дает
возможность записать производную
следующим образом:
|
|
Свойство дифференцируемости функции
- Теорема 5.2 (Ролля)
Пусть
функция 
дифференцируема
на интервале 
,
непрерывна в точках 
и 
и
принимает в этих точках значение 0: 
.
Тогда найдётся хотя бы одна точка 
,
в которой 
.
- Теорема 5.3 (Лагранжа)
Пусть
функция 
дифференцируема
на интервале 
и
непрерывна в точках 
и 
.
Тогда найдётся такая точка 
,
что
|
|
- Теорема 5.4 (Коши)
Пусть
функци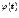и 
и 
дифференцируемы
на интервале 
и
непрерывны при 
и 
,
причём 
при
всех
.
Тогда в интервале 
найдётся
такая точка 
,
что
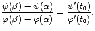
19.
Правило дифференцирования суммы функций:
Правило дифференцирования
разности функций:
Правило дифференцирования
произведения функций (правило Лейбница):
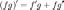
Правило дифференцирования
частного функций:
20.Правило
дифференцирования сложной функции.Сложная
функция (композиция функций, суперпозиция
функций) обозначается
или
.
Производная композиции
равна: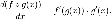
Если необходимо взять
производную от композиции трех и более
функций, то последовательно применяем
указанное выше правило. Например,
Рассмотрим дифференциал
функции
в произвольной точке промежутка
:
.
Здесь
-
приращение независимой переменной,
которое является числом и не зависит
от
.
Пусть теперь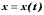
-
функция независимого переменного
,
определенная на промежутке
.
Тогда
-
сложная функция переменного
.
Вычислим ее дифференциал, используя
формулу для производной сложной функции:
.
Заметим, что
и
выражение для дифференциала принимает
ту же форму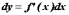
,
хотя здесь
уже
функция переменного
.
Это свойство дифференциала первого
порядка называется инвариантностью
(т.е. неизменностью) его формы. При
вычислении дифференциала второго
порядка придется учитывать, что
-
функция переменного
.
Поэтому
и
форма второго (а также и всех следующих)
дифференциала неинвариантна.
21. Связь между производными взаимно-обратных функций. Записывают это так:
или
,
где индексы
и
показывают
по какой переменной производится
дифференцирование, т. е. какая из перемен
принята за независимую.
Связь между производными взаимно обратных функций весьма наглядно иллюстрируется геометрически.
22.
Производные основных элементарных
функций.