7.5.3. Невласні інтеграли від необмежених функцій.

Розглянемо необмежену функцію , задану у скінченному проміжку . Нехай обмежена й інтегровна у будь-якому проміжку та необмежена у кожному проміжку зліва від точки (). Точку називають у цьому випадку особливою точкою.

Границя інтеграла при (скінченна або нескінченна) називається невласним інтегралом функції від до і позначається:

. (7.17)

Якщо ця границя скінченна, то кажуть, що інтеграл (7.17) збігається, а функцію називають інтегровною у проміжку . Якщо ж границя (7.17) нескінченна або не існує, то про інтеграл кажуть, що він розбігається.

Геометрично інтеграл (7.17) при визначає площу криволінійної трапеції, обмеженої графіком функції , прямими , та віссю .

Приклад 7.12. Дослідити на збіжність невласний інтеграл:

.

Розв’язок. Функція обмежена та інтегровна у будь-якому проміжку () і перетворюється у нескінченність при . Точка є особливою точкою.

.

Невласний інтеграл збігається і його значення дорівнює .

Аналогічно визначають невласний інтеграл, коли особливою точкою є нижня границя інтеграла (точка ) або точка , що лежить у середині інтервалу . В останньому випадку невласний інтеграл

.

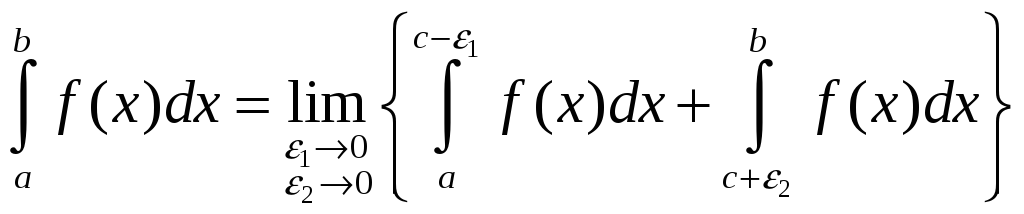Графік підінтегральної функції подано на рис. 7.7.

З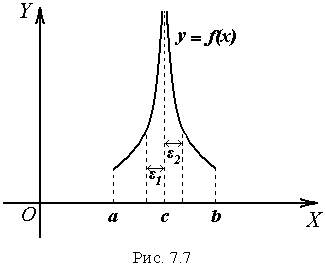астосування формули Ньютона-Лейбніца дозволяє одночасно з’ясувати збіжність невласного інтеграла і знайти його значення. Для цього необхідно, щоб первісна , що має усюди, виключаючи особливі точки, своєю похідною функцію , була сама неперервна у цих особливих точках.

Так, якщо у особливій точці існує границя , то невласний інтеграл (7.17) обчислюють за формулою

.

Приклад 7.13. Дослідити при яких значеннях параметра збігається невласний інтеграл

, (). (7.18)

Розв’язок. Точка є особливою. Інтеграл ()

при має границю , якщо , і скінченне число , якщо . Якщо ж , то

.

Отже, невласний інтеграл (7.18) при  збігається, а при розбігається.

У більш складних випадках, холи первісна функція невідома, при з’ясуванні збіжності невласного інтеграла слід дослідити поведінку підінтетральної функції поблизу особливої точки

,

і скористатися теоремою порівняння, згідно з якою інтеграли та одночасно або збігаються або розбігаються.

Приклад 7.14. Дослідити збіжність інтеграла

.

Розв’язок. Точка є особливою:

.

Інтеграл розбігається (див. попередній приклад), отже, за теоремою порівняння, розбігається й інтеграл .

7.6. Застосування визначеного інтеграла.

Слід звернути увагу на схему, за якою у прикладних питаннях звичайно приходять до необхідності упровадження визначеного інтеграла при обчисленні тих чи інших величин.

Нехай  деяка величина, що має властивість адитивності на інтервалі . Це означає, що, якщо проміжок складається з частин , , , , , , то величину можна подати сумою , де елемент величини відповідає проміжку . За величину можна, наприклад, взяти довжину, площу, об’єм (у геометричних застосуваннях), масу, роботу, заряд і т.ін. (у фізичних застосуваннях).

Покладаючи досить малими, знаходять для наближене значення, лінійне відносно :

, ().

Суму можна розглядати як інтегральну суму (див. розд.7.І) і, переходячи у ній до границі (), для величими отримують точний вираз у вигляді визначеного інтеграла

.

7.6.1. Обчислення площі плоских фігур.

а) Інтеграл

(7.19)

визначає (див. розд.7.І) площу криволінійної трапеції (рис.7.І), обмеженої кривою та прямими , , .

Якщо крива, що обмежує плоску фігуру, задана параметрично: ; ; , то, роблячи заміну змінної у інтегралі (7.19), одержимо:

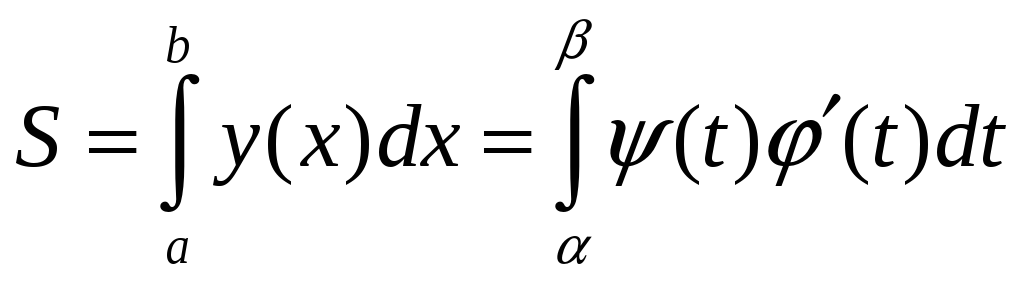, (7.20)

де ; .

Приклад 7.15. Обчислити площу фігури, обмеженої аркою циклоїди , ; (рис. 7.8)

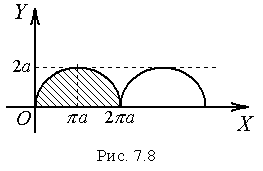Розв’язок. Згідно з формулою (7.20) маємо:

.

б) Нехай крива задана в полярній системі координат рівнянням , де  неперервна функція при . Елемент площі , що відповідає інтервалу кутів буде

.

Тоді площа сектора в інтервалі кутів буде:

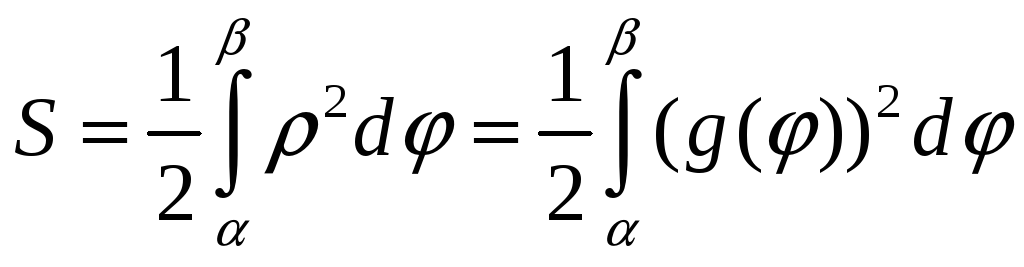. (7.21)

Приклад 7.16. Знайти площу одного витка архімедової спіралі .

Розв’язок. Згідно з формулою (7.20) маємо:

.

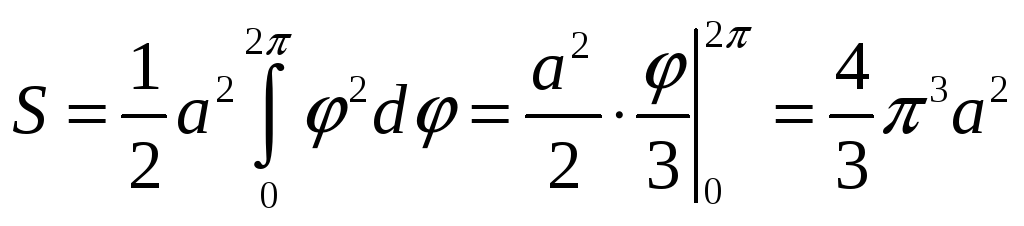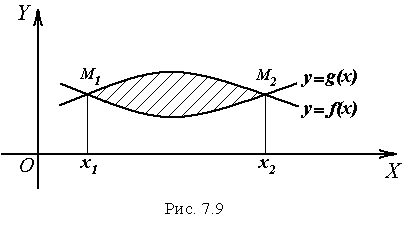
в) Задача обчислення площі плоскої фігури, обмеженої двома кривими та (рис. 7.9), зводиться до обчислення інтеграла

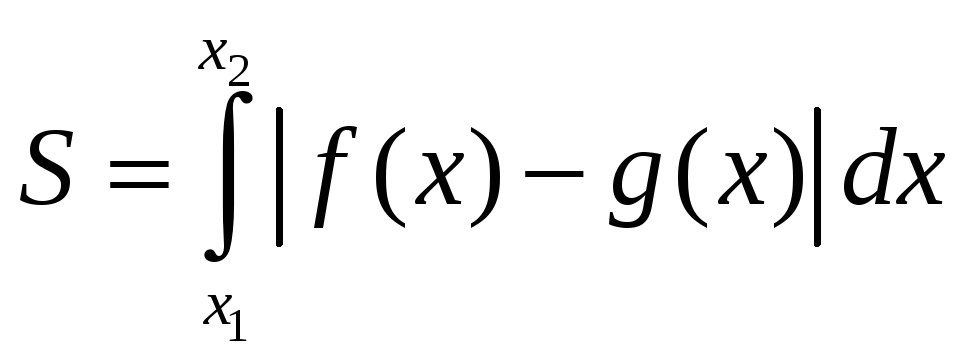, (7.21)

де, координати і точок і перетину даних кривих визначають розв’язуючи рівняння .

Приклад 7.17. Обчислити площу фігури, обмеженої параболами та .

Розв’язок. Покладаючи та і визначивши з рівняння абсциси точок перетину парабол і , згідно з формулою (7.22) одержимо:

.

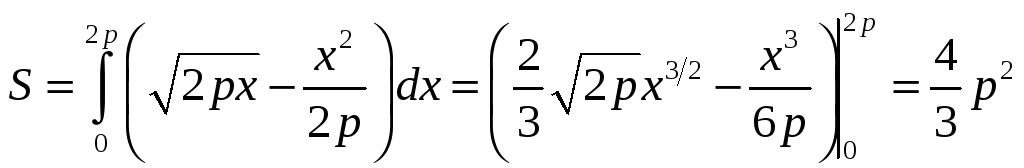Зробіть малюнок фігури, розглянутої у даному прикладі.

7.6.2. Обчислення довжини кривої.

а) Нехай плоска крива задана параметрично: ; ; , де функції і та їхні похідні неперервні.

Довжина дуги кривої визначиться інтегралом

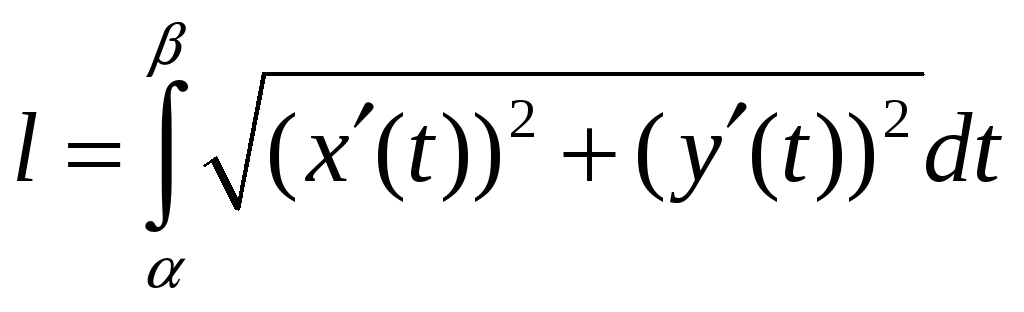, (7.23)

де , .

Приклад 7.18. Обчислити довжину однієї арки циклоїди , ; (див. рис. 7.8).

Розв’язок. Так як , . Тоді, згідно з формулою (7.23) маємо:

.

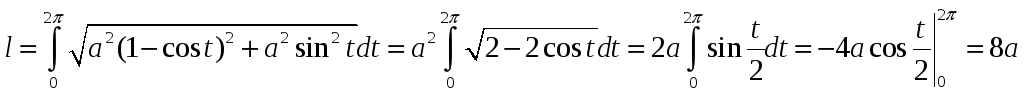б) Нехай плоска крива задана рівнянням , де функція та її прохідні неперервні на відрізку . Обравши за параметр: , , з формули (7.23) одержимо

. (7.24)

Приклад 7.19. Знайти довжину дуги ланцюгової лінії на інтервалі осі абсцис.

Розв’язок. Так як , , то з формули (7.24) одержимо:

,

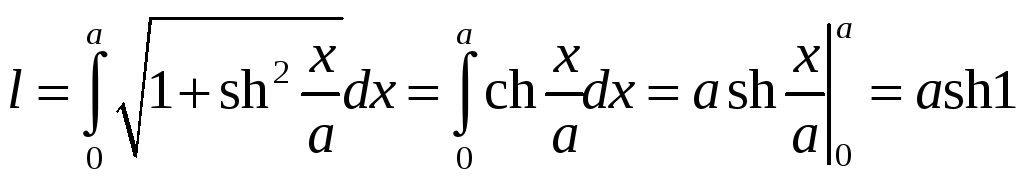де  гіперболічний синус;  гіперболічний косинус.

в) Нехай плоска крива задана в полярних координатах рівнянням ; . Використовуючи зв’язок декартових координат з полярними

та, розглядаючи кут як параметр, з формули (7.23) маємо:

. (7.25)

Виведіть цю формулу.

П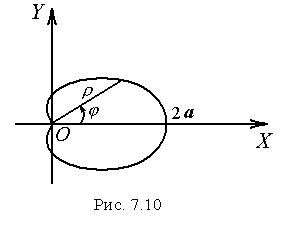риклад 7.20. Знайти довжину кардіоїди , (рис. 7.10).

Розв’язок. Так як , , то, згідно з формулою (7.25) маємо:

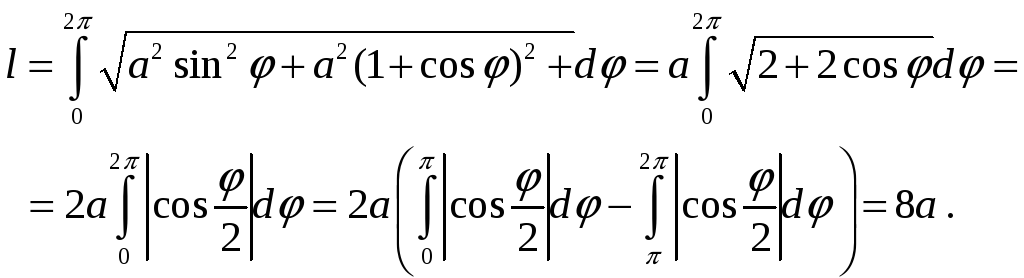
г) Досі розглядались криві, що лежать у площині. Нехай просторова крива задана параметричними рівняннями ; ; ; , де функції , , та їхні похідні неперервні.

Довжина дуги кривої визначиться інтегралом

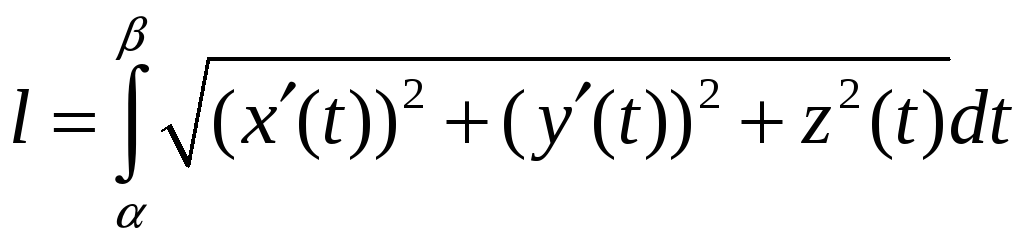, (7.26)

де , , .

Приклад 7.21. Обчислити довжину гвинтової лінії , , ; .

Розв’язок. Так як , , , то, згідно з формулою (7.26) маємо:

.

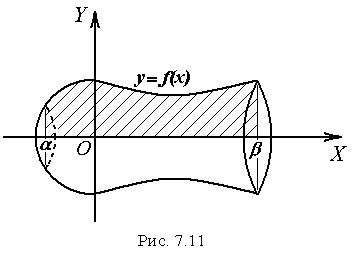
7.6.3. Об’єм тіла обертання.

Нехай фігура обертається довкола осі . Об’єм тіла, утвореного обертанням фігури довкола осі (рис. 7.11) дорівнює:

.

.

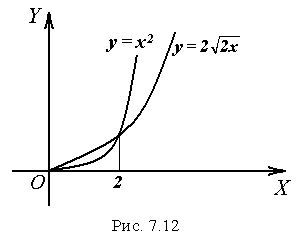
Приклад 7.22. Обчислити об’єм тіла, утвореного обертанням довкола осі фігури, обмеженої параболами та (рис. 7.12).

Розв’язок. Знаходимо точки перетину парабол:

.

Шуканий об’єм тіла обертанням буде дорівнювати:

,

тобто дорівнює різниці об’ємів тіл, утворених відповідно обертанням фігури та фігури .

7.6.4. Приклади фізичних застосувань визначеного інтеграла.

1) Робота змінної сили , що діє у напрямку осі на відрізку :

.

Приклад 7.23. Яку роботу треба виконати, щоб розтягнути пружину на , якщо відомо, що від навантаження вона розтягується на ?

Розв’язок. Згідно з законом Гука сила . Коефіцієнт знайдемо з умови: якщо , то , отже, і . Тоді

.

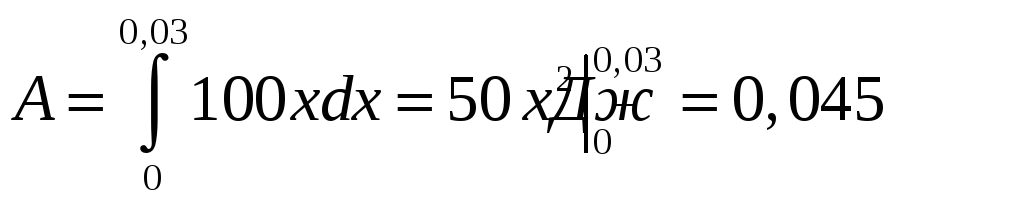2) Знаходження статичних моментів та центра тяжіння плоскої фігури. Розглянемо плоску фігуру (рис.7.13), обмежену зверху кривою , яка задана рівнянням . Покладемо, що маса розподілена по данній фігурі рівномірно зі сталою поверхневою густиною (заради простоти вважаємо ). Статичні моменти і цієї фігури відносно осей координат визначаються інтегралами

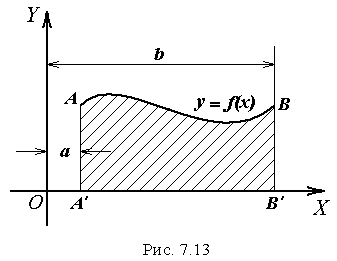, , (7.27)

а координати та центра тяжіння фігури  формулами

, ,

де  маса фігури

.

Приклад 7.24. Знайти статичні моменти , і координати , центра тяжіння фігури, обмеженої параболою , віссю та прямою .

Розв’язок. З того, що , за формулами (7.27) маємо:

, .

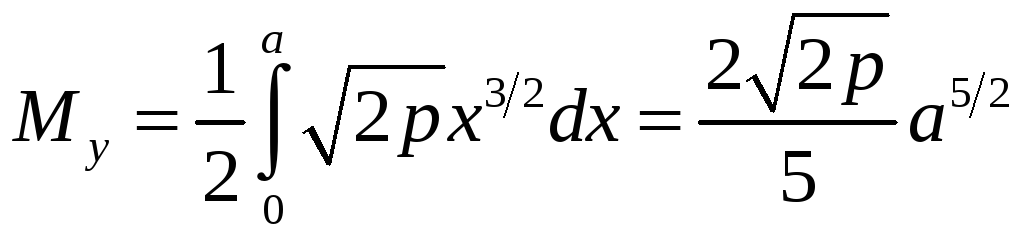Оскільки

,

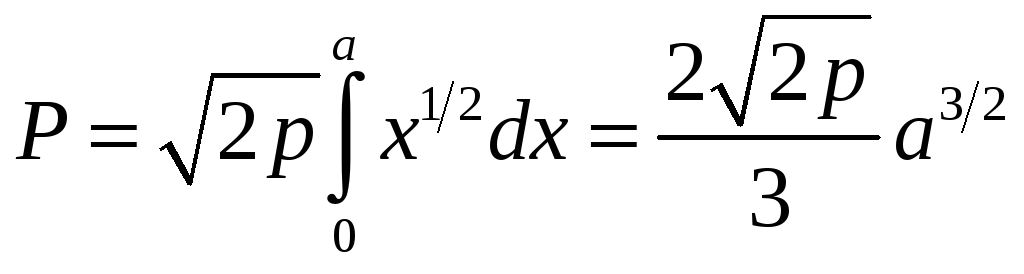для координат центра тяжіння за формулами (7.28) знаходимо:

, .

Питання для самоперевірки.

1. Що називається інтегральною сумою? Побудуйте ескіз інтегральної суми для додатної функції.

2. Що називається визначеним інтегралом? Наведіть приклад.

3. Які функції називаються інтегровними? Наведіть приклади інтегровних функцій.

4. Сформулюйте властивості визначеного інтеграла при перестановці границь інтегрування.

5. Сформулюйте (з наведенням рисунків) наближені методи обчислення інтегралів. Який з них дає більшу точність?

6. Як оцінити похибку чисельного інтегрування?

7. Які властивості визначених інтегралів відображаються рівностями, а які нерівностями?

8. Сформулюйте теореми про середнє значення.

9. Що називається формулою Ньютона-Лейбніца?

10. Які властивості має інтеграл як функція верхньої границі?

11. Як зробити заміну змінної величини у визначеному інтегралі? Чи треба переходити до старої змінної величини?

12. Як робиться інтегрування частинами у визначеному інтегралі?

13. Як обчислюється площа криволінійної трапеції, обмеженої кривою, заданою в декартових координатах, параметрично і в полярних координатах?

14. Як обчислюється площа фігури, обмеженої двома кривими? Наведіть приклад.

15. Як обчислюється довжина дуги кривої, заданої в декартових координатах, параметрично і в полярних координатах?

16. Як обчислюється об’єм тіла обертання?

17. Які інтеграли звуться невласними?

18. Як застосовується формула Ньютона-Лейбніца при обчисленні невласних інтегралів?

19. Сформулюйте теореми порівняння. Як досліджується збіжність невласних інтегралів?

Л і т е р а т у р а: [4, гл. 6, § 6; 5, гл. 7, § 7.1-7.3; 6, гл. ХII, § 1-5].

112