7.4.2 Інтегрування частинами.
Нехай
функції
і
диференційовні на інтервалі
.
Тоді:
,
або
.
Приклад
7.7.
Обчислити
визначений
інтеграл
.
Розв’язок. Обчислимо інтеграл, зробивши заміну змінної інтегрування.
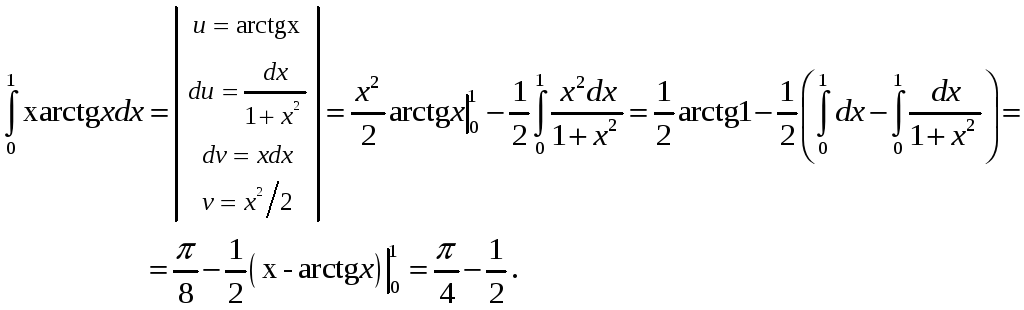
7.4.3 Наближене обчислення визначених інтегралів.
Точне обчислення визначених інтегралів можливо для функції з відомою первісною (формула Ньютона-Лейбніца) або з використанням спеціальних засобів. У більшості випадків, що мають прикладне значення, доводиться обмежуватися методами наближеного обчислення інтегралів.
Зверніть
увагу на такі методи,
що
найчастіше використовуються, у яких
наближені
формули для інтегралів складаються за
набором
значень підінтегральної функції
,
обчислених для сукупності (як правило,
рівновіддалених) значень незалежної
змінної.
Формула
трапецій.
Впишемо у криву
ламану лінію
з
вершинами у точках
(
).
Замінюючи
площу фігури
наближено сумою площ трапецій (рис.
7.4), для
визначеного
інтеграла отримаємо наближену формулу
,
(7.10)
що
називається формулою трапецій. Тут
,
.
Додатковий
член
,
що визначає похибку формули (7.10),
описується таким виразом
,
де
,
(7.11)
у
припущенні, що функція
в проміжку
має неперервні похідні двох порядків.
Із
зростанням
похибка
формули трапецій (7.10)
спадає приблизно як
(оскільки у загальному випадку величина
в
формулі (7.11)
залежить
від
,
тому не можна говорити про точну
залежність
).
Формула парабол (формула Сімпсона). Ця формула дозволяє одержати більшу в порівнянні з формулою трапецій (7.10) точність (при тому ж обсязі обчислень).
Розділимо
інтервал
на
парне число
(
)
рівних частин. Криву
на кожній парі відрізків ділення
і
(
)
замінимо
параболою,
що
проходить через точки
,
та
.
Площа
фігури, обмежена
параболою
та
прямими
,
,
(рис.
7.5).
.
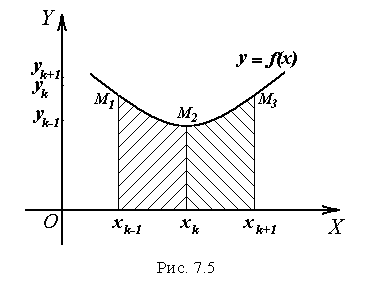
Шуканий інтеграл визначиться сумою вказаних площ, в результаті одержимо формулу Сімпсона:
.
(7.12)
Додатковий
член
,
що визначає похибку формули (7.12),
описується таким виразом
,
де
(7.13)
і
спадає приблизно як
зі зростанням
.
Оцінка
похибки чисельного інтегрування.
Застосування методів наближеного
обчислення інтегралів викликає
необхідність у оцінці допущеної при
цьому похибки
.
У формулах трапецій (7.10)
і парабол (7.12)
похибка
,
де
визначається відповідно формулам (7.11)
і
(7.13),
що дає можливість визначити похибку
наближення при фіксованому значенні
або обрати таке значення
,
що забезпечує потрібну точність.
Приклад
7.8.
Обчислити
визначений
інтеграл
з
точністю до
за формулою Сімпсона.
Розв’язок.
Оскільки
,
,
при
,
то з формули (7.4) маємо:
.
Покладемо
.
Тоді
;
;
;
;
;
.
За формулою (7.12)
знаходимо:
Оцінити
похибку чисельного інтегрування можна
й іншим способом. Позначимо через
праву частину у формулах (7.10)
і (7.12).
Обчислюємо
,
подвоюючи на кожному етапі число
розбиття проміжку
на рівні частини. Обчислення продовжимо
доти, поки не буде виконане співвідношення
,
де
для формули трапеції;
для формули Сімпсона. Вказаний спосіб
зветься способом Рунге.
Л і т е р а т у р а: [4, гл. 6, §4, п. 4.5; 5, гл. 6, §6.4, гл. 7, §7.7-7.8; 6, гл. ХI, §5,6,8].