11. Свойства сходящихся рядов.
1.
а1+а2+...+an+…=
(1), если ряд сх-ся имеет сумму S,
то kа1+kа2+...+kan+…=
(2),
так же сходится и имеет сумму kS.
Если ряд один расходится, то при k≠0 ряд (2) также будет расходящимся.
2. Сходящиеся ряды можно почленно складывать, при этом сумма нового ряда будет рана сумме сумм слагаемых.
3. Если к ряду прибавить или отбросить конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.
12. Необходимый признак сходимости ряда.
Если ряд сходится, то …
Обратное утверждение не верно, примером является гармонический ряд.
Следствие
1. Если
,
то ряд расходится ….
Следствие
2. Если
,
то ряд может как сходиться, так и
расходиться…..
Доказательство:
Рассмотрим:
-сходящийся
ряд
.
.
13. Гармонический ряд.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
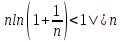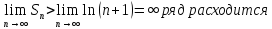ю
14. Признаки сравнения положительных рядов.
Первый признак сравнения.
Пусть
даны 2 положительных ряда
.
Тогда из сходимости ряда 2, следует, сходимость ряда 1, а из расходимости ряда 1, следует, расходимость ряда 2.
Это признак можно сформулировать и так: если сходится ряд с большими членами, то сходится ряд с меньшими.
Если расходится меньший ряд, то расходится и больший.
Доказательство:
Т.к.
ряд 2 сходиться, то существует ряд
.
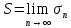Последовательность
монотонно
возрастает, т.к. ряд положительный. Если
Sn-частичная
сумма ряда 1, то
.
.
,значит последовательность Sn – ограниченная последовательность, если последовательность монотонная и ограниченная сверху числом S, то по теореме Вейрштрасса она имеет предел и, значит, ряд 1 сходится.
Покажем, что из расходимости ряда 1 следует расходимость ряда 2.
.
или не существует.
или не существует.
Следовательно, ряд расходится.
Второй признак сравнения.
Если an и bn положительные ряды, если существует конечный предел отношения этих рядов, не равных 0, то оба ряда сходятся или расходятся одновременно.
.
15. Признак Даламбера, радикальный признак Коши.
Признак Даламбера.
Пусть
- положительный,
.
Тогда, если l<1,
то сходиться, если l>1,
- расходится, если l=1,
то может сходиться и расходиться, т.е.
признак ответа не дает.
Замечание 1. Признак Даламбера обычно дает ответ на вопрос о сходимости ряда, если в запись общего члена ряда входит показательная функция или факториал.
Радикальный признак Коши.
Пусть
ряд an
– положительный и
,
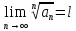тогда, если:
l<1, то ряд сх-ся,
l>1, то ряд расх-ся,
l=1, признак ответа не дает.
Замечание.
Радикальный признак Коши, как правило, применяют тогда, когда an представляет собой более высокую степень некоторого выражения.
16. Интегральный признак Коши, обобщенный гармонический ряд.
Пусть
-положительный
ряд.
f(n)=an, f(x)-непрерывна и убывающая на интервале [1;∞)
–сходятся или
расходятся одновременно.
Доказательство:
1.
– сходится.
.
Т.к. интеграл сходится, то частичная
сумма Sn
монотонно возрастает и ограничена
сверху, поэтому limSn
существует
и конечен, т.е. ряд сходится.
2.
Если
–расходящийся, то
–сходится.
.
.
- ряд расходится.
Обобщенный гармонический ряд.
–называется
обобщенным гармоническим рядом.
Выясним,
при каких значениях р ряд сходиться
– непрерывная и
убывающая на промежутке [1;+∞)
.
.
1.
.
2.
.
Интеграл сходиться, если р>1, интеграл расходиться, если р<1, значит ряд сходиться, если р>1, расходиться, если р<=1.