
- •1. Ду первого порядка с разделяющимися переменными и однородные.
- •2. Линейные ду первого порядка. Уравнение Бернулли.
- •3. Ду в полных дифференциалах.
- •4. Уравнения допускающие понижение порядка.
- •5. Линейные однородные ду 2-го порядка с постоянными коэффициентами.
- •6. Линейные однородные уравнения n-го порядка с постоянными коэффициентами.
- •7. Линейные неоднородные ду с постоянными коэффициентами, теорема о структуре решений.
- •8. Метод вариации Лонгранжа.
- •9. Линейные неоднородные ду с правой частью специального вида.
- •10. Числовые ряды, частичная сумма, сходящиеся и расходящиеся ряды, геометрические ряды.
- •11. Свойства сходящихся рядов.
- •12. Необходимый признак сходимости ряда.
- •13. Гармонический ряд.
- •14. Признаки сравнения положительных рядов.
- •15. Признак Даламбера, радикальный признак Коши.
- •16. Интегральный признак Коши, обобщенный гармонический ряд.
- •17. Абсолютно и условно сходящиеся знакопеременные ряды.
- •18. Достаточный признак сходимости з.П.Р.
7. Линейные неоднородные ду с постоянными коэффициентами, теорема о структуре решений.
Такие
уравнения имеют вид
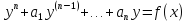 (1)
(1)
Теорема о структуре решения линейного неоднородного уравнения.
Если У – общее решение соответствующего однородного уравнения,
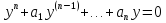 (2)
(2)
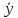 -некоторое
частное решение неоднородного уравнения
(1), то
-некоторое
частное решение неоднородного уравнения
(1), то
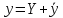 является общим решением уравнения (1).
является общим решением уравнения (1).
Докажем теорему для линейного неоднородного уравнения второго порядка.
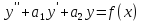
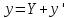 , где У - общее
решение.
, где У - общее
решение.
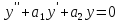 ,
,
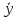 -
частное решение,
-
частное решение,
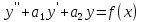
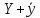 -решение
уравнения
-решение
уравнения
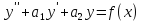
y=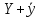 ,
,
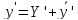 ,
,
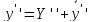
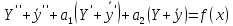
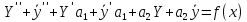
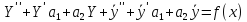
Т.к.
У - общее решение, то первая скобка равна
0, т.к.
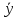 –
общее решение, то вторая скобка равна
f(x).
–
общее решение, то вторая скобка равна
f(x).
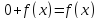
Покажем, что входящие в решение произвольные постоянные можно выбрать так, чтобы были выполнены начальные условия
у(х0)=у0
х(у0)=х0
Каковы
бы ни были числа х0, у0,
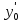
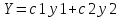 ,
где у1 и у2 ФСР однородного уравнения.
,
где у1 и у2 ФСР однородного уравнения.
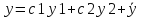
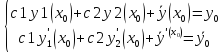
Это система линейных уравнений относительно с1 и с2 с определителем отличным от 0.

Т.к.
определитель
 является определителем Вронского для
функции у1 и у2, которые линейно не
зависимы.
является определителем Вронского для
функции у1 и у2, которые линейно не
зависимы.
Полученная система является Крамеровской и всегда имеет единственное решение.
Теорема.
Если
у1(х) – решение уравнения
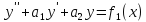 ,
у2(х) – решение уравнения
,
у2(х) – решение уравнения
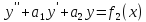 ,
то у=у1(х)+у2(х) – является решением
уравнения.
,
то у=у1(х)+у2(х) – является решением
уравнения.
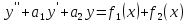
Доказательство:
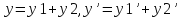 ,
,
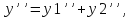
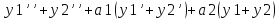 =
=
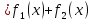
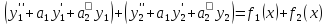
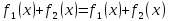
8. Метод вариации Лонгранжа.
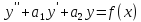 (1)
(1)
Соответствующие однородные уравнения имеют общее решение
Y=c1y1+c2y2, тогда частное решение неоднородного уравнения
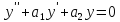 (2), тогда частное
решение неоднородного уравнения
(2), тогда частное
решение неоднородного уравнения
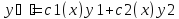
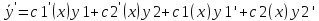
Пусть
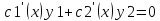
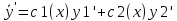
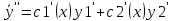
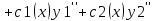
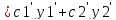
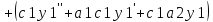
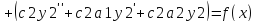
Т.к.
у1-решение уравнения
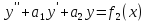 и у2-решение этого же уравнения, то
первая и вторая скобки равны 0.
и у2-решение этого же уравнения, то
первая и вторая скобки равны 0.
Таким образом, для нахождения с1(х) и с2(х) получена система.
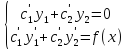
Полученная
система является крамеровской, из этой
системы
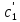 и
и
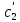 определяются однозначно проинтегрировав
полученные функции найдем с1(х) и с2(х)
и найдем частное решение неоднородного
уравнения
определяются однозначно проинтегрировав
полученные функции найдем с1(х) и с2(х)
и найдем частное решение неоднородного
уравнения
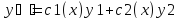
9. Линейные неоднородные ду с правой частью специального вида.
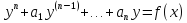 ,
где
a1, a2,…., an-const
,
где
a1, a2,…., an-const
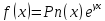 или
или
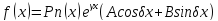
Частное
решение неоднородного уравнения будет
иметь такой же вид как и правая часть
только многочлен соответствующей
степени будет полный и м.б. решение
будет умножено на
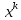 .
.
Пусть Qn(х) – полный многочлен степени n,
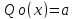 ,
,
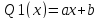 ,
,
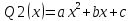
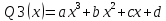
1.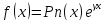 не является корнем соответствующего
характеристического уравнения, то
не является корнем соответствующего
характеристического уравнения, то
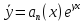
γ - корень характеристического уравнения, кратности k
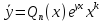
2.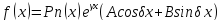
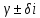 -не
корень характеристического уравнения.
-не
корень характеристического уравнения.
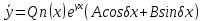
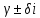 -корень
характеристического уравнения, кратности
k,
то
-корень
характеристического уравнения, кратности
k,
то
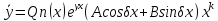
10. Числовые ряды, частичная сумма, сходящиеся и расходящиеся ряды, геометрические ряды.
а1, а2,.., аn, ...-последовательность,
а1+а2+...+an+…=
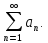
а1, а2, … -члены ряда.
Ряд считается заданным, если известен закон, по которому можно найти любой член ряда.
аn - общий член ряда.
Сумма
первых n-членов
ряда S=
а1+а2+...+an
и называется n-ой
частичной суммой ряда, такой предел
называют суммой ряда
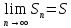
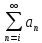 =S
=S
Ряд называется расходящимся, если предел последовательности частичных сумм ряда бесконечен или существует.
Предел последовательности четных частичных сумм будет равен 0, а предел последовательности нечетных частичных сумм равен 1, т.к. из последовательности частичных сумм выделены 2 сходящиеся и расходящиеся предела, то предел такой последовательности не существует, следовательно, ряд расходится.
Геометрическим рядом называется ряд, составленный из членов бесконечной геометрической прогрессии.
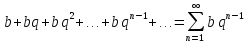
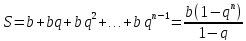
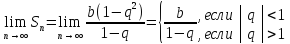
Геометрический ряд сходится, если │q│<1 и расходится, если │q│>1
