2 Вопрос.

Уравнение прямой проходящей через данную точку в за-ом направлении.

А(x0:y0), К - заданное направление

y B(x:y) - произвольная

y0 A y-y0

x-x0 заданное

x0 x

K= y-y0 / x-x0

y-y0=K*(x-x0)

пример:

Напишите уравнение прямой проходящей через зад. Точку перпендикулярной данной прямой с заданным К

А(x0:y0)

К= -1/К1

y-y0 = -1/ К1 и эту дробь умножить на (x-x0)

3билет

Уравнение прямой, проходящей через 2 заданные точки.

Рассмотрим на примере: пусть 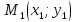и 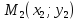- точки лежащие на одной прямой. Найдём k - угловой коэффициент:

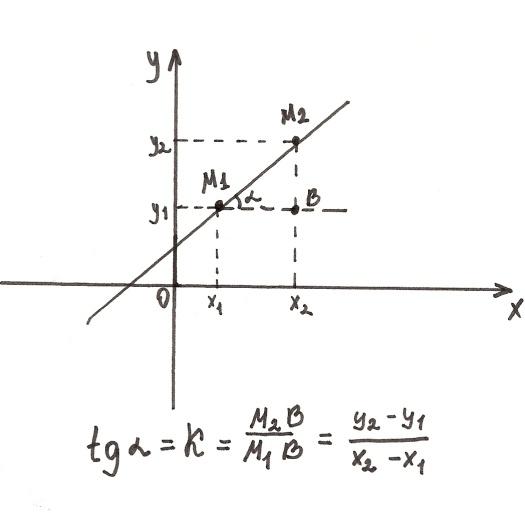
Теперь мы можем записать искомое уравнение прямой в форме прямой, проходящей через точку 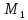в заданном направление:

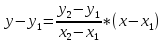
4билет

Уравнение прямой в отрезках.

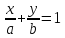
Докажем, что это действительно уравнение для прямой:

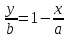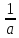
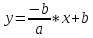, k = -

, k = - 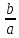доказано.

Выясним смысл параметров a и b:

1. Пусть у=0, тогда 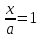, х = а. Значит этой прямой принадлежит точка (а;0)

2. Пусть х = 0, тогда 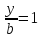, y = b. Значит этой прямой принадлежит точка (0;b)

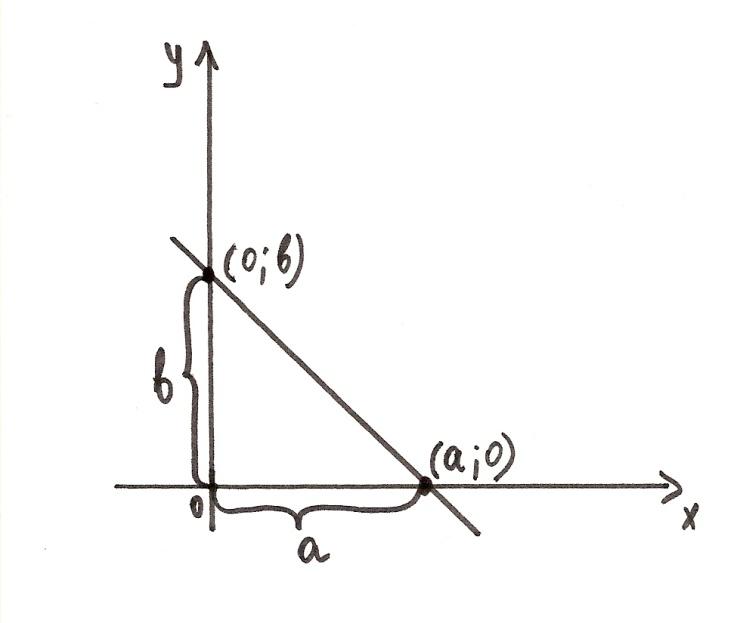
Геометрический смысл параметров а и b: это отрезки, отсекаемые прямой от осей координат.

Формулой:

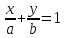
Можно задать любую прямую!

Билет №5 Парабола. Уравнение параболы.

Парабола - геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Свойства:

• парабола — кривая второго порядка.

• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.

• Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

• Для параболы 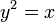фокус находится в точке (0,25; 0).

Для параболы фокус находится в точке (0; f).

• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

• Парабола является антиподерой прямой.

• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Уравнения:

Каноническое уравнение параболы в прямоугольной системе координат:

(или , если поменять местами оси).

Эксцентриситет:

Билет№6.Эллипс. Уравнение эллипса.

Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами эллипса, есть величина постоянная.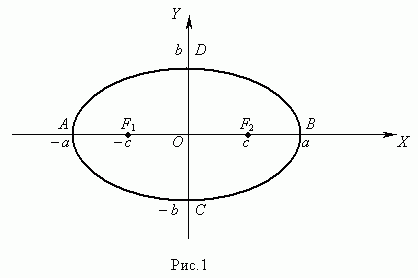

Уравнение эллипса

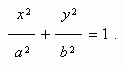
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса. Отрезок F1F2 = 2 с , где называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.

Пусть Р ( х1 , у 1 ) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид: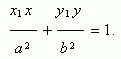

Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1 :

k ² = m ² a ² + b ² .

Билет № 7 Гипербола. Уравнение гиперболы.

(r₁-r₂)=2a

(Выражение все под корнем до минуса и после) √(x+c)²+y²-√(x-c)²+y²=+2a -2a

После преобразования связанных с преобразованием радикалов

(с²-а²)х²-а²у²=а²(с²-а²)

b²=(c²-a²)

b²x²-a² y²=a² b²

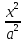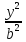^{- =1}

Билет №8 Векторное произведение векторов. Свойства векторного произведения.

Скалярное произведение векторов.

напоминаю косинус между ними.

Свойство скалярного произведения.

Текстом нашла:

1)переместительное свойство умножения

2)распределительное