Кафедра Энергетики Краткий конспект лекций по электротехнике для специальностей ртп, ртб, ртмо

Лектор : профессор Меньков Б.В.

Москва 2007 г.

Компьютерная графика выполнена студентами:

Кислицын И.Э, Борисов Д.Г, Набока Р.Р., Семенова К.М (все РТМО-05), Пустовая Л.Г., Потапов К.С.(оба РТБ-05-1), Минькеева И. (РТП-05), Абранин А. (РТБ-05-2).

Текст лекций сохранен, в основном, по студенческим конспектам.

Электротехника – эта отрасль науки и техники, которая занимается производством передач и переходов тока при управлении электрической энергии.

Расчеты сводятся по заданным значениям ЕДС напряжения, определяя токи и мощи потребителя. Токи определяем, для того чтобы по известной плотности тока и сопротивлению определять их сечения и габарит, т.е. нагрузка в электротехнике – это величины тока и мощности, но не напряжения. Напряжение не является нагрузкой.

В природе существуют три главных типа нагрузки:

1. Сопротивление 2. Индуктивность 3. Ёмкость

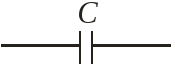
Элементы электрической цепи.

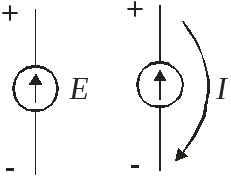
ЭДС источника может быть замерена вольтметром в режиме холостого хода, когда ток равен нулю. (R₀ = 0)

Уравнение баланса мощностей

Этим уравнением должен заканчиваться каждый электротехнический расчёт.

Соединения различных элементов называются электрической цепью, а графическое изображение цепи – электрической схемой. Электрические схемы могут быть принципиальными, расчетными ( замещения) и монтажными.

Электрическая схема показывает, как осуществляется соединение элементов рассматриваемой цепи. В электрической схеме соединения элементов образуют ветви, узлы, контуры.

Участок электрической цепи, по которому проходит ток одного и того же значения и направления, называется ветвью.

Замкнутая электрическая цепь, образованная одной или несколькими ветвями, называется контуром, а место соединения трёх или более ветвей – узлом. На схеме узел изображается точкой.

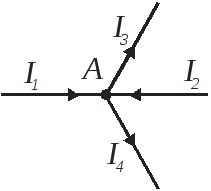
Вся электротехника базируется на двух законах Кирхгофа. Оба закона были установлены на основании многочисленных опытов и потому получили название

Опытные Законы Кирхгофа.

Опытные Законы Кирхгофа.

Согласно I-му закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю:

∑ Iκ = 0

І₁+І₃-І₂-І₄=0

Согласно II-му закону Кирхгофа алгебраическая сумма ЭДС источников питания в любом контуре равна алгебраической сумме падений напряжения на элементах этого контура.

ΣЕ=ΣU

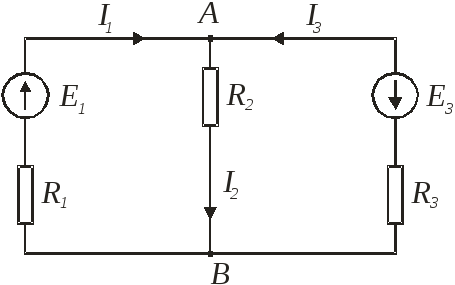
При расчете по первому закону Кирхгофа составляется число уравнений на единицу меньше числа узлов. Перед расчетом назначаются условно положительные направления.

І₁+І₃- І₂=0 (1)

Число уравнений должно быть равно числу ветвей.

Для любого замкнутого контура нужно выбрать направление обхода. Направление обхода по часовой стрелке.

Е1=І1 · R1+ І2 · R2 (2)

Е1+ Е3= І1 · R1- І3 · R3 (3)

Решая эти уравнения мы определяем токи І1, І2, І3; если получилось со знаком «+», то действительное (расчетное) направление тока совпадает с назначено ранее условноположительным направлением ветвей, если со знаком «-», то условноположительное направление ветвей необходимо поменять на обратное.

По известному значению плотности тока, мы определяем S=І / q.

Расчет заканчиваем уравнением баланса мощностей.

Правило:

При составлении уравнений по второму закону Кирхгофа в каждое последующее уравнение необходимо вводить дополнительный контур или одну из ветвей, чтобы не было уравнений тождественных.

Для уменьшения вычислительной работы по первому закону Кирхгофа, предложено ряд методов, основанных на применение законов Кирхгофа.

Метод контурных токов.

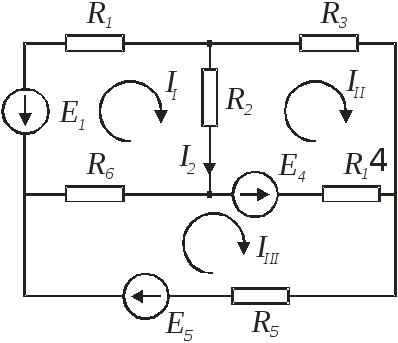
Три расчетных контура по которым протекает свой контурный ток. По первому закону Кирхгофа составляем три уравнения, и по второму закону Кирхгофа – три уравнения. Общее число ветвей 6.

Е1= І1·( R1+ R2 + R6) – ІІІ· R2 – ІІІІ·R6;

- E4=ІІІ· (R2+R3+R4) – ІІ·R2 – ІІІІ·R4 ;

E4+E5=ІІІІ· (R4+R5+R6) – ІІ·R6 – ІІІ·R4 ;

Решая эти уравнения определяем контурные токи.

Правило знаков:

Для определения действительных токов в ветвях, ток в не разветвленной ветви равен контурному, если контурный ток получился со знаком «+», если контурный ток со знаком «-», то равен контурному, но направлен в противоположную сторону.

В смежных ветвях действительный ток равен алгебраической сумме смежных контурных токов.

Знак алгебраической суммы определяется направлением первого тока в правой части.

Расчет заканчиваем уравнением баланса мощностей для действительных токов.

Метод двух узлов или узлового напряжения.

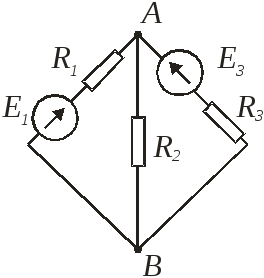
Если ЭДС направлена в сторону положительного узла со знаком (+), и наоборот со знаком (-). Расчет заканчивается уравнением баланса мощностей.

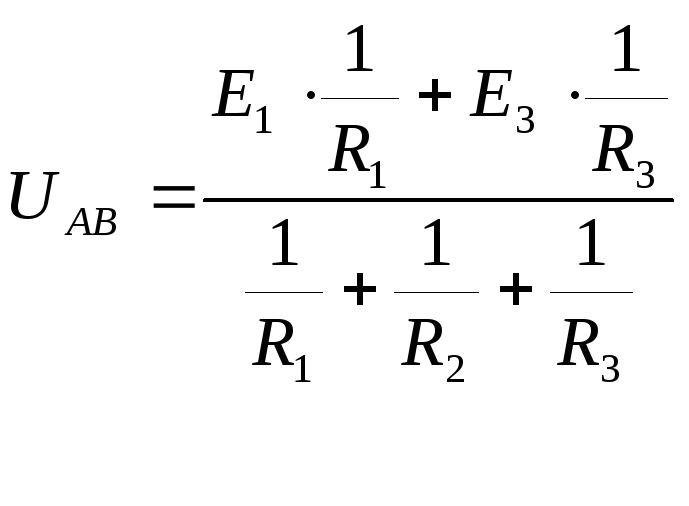
Токи в ветвях определяются по закону Ома.

Электрические цепи бывают: простые и сложные. Простые, когда один источник электрической энергии и схему можно свернуть (упростить) до минимального параметра L,R,C. Сложные – когда с двумя или более источниками электрической энергии.

При свертке можно преобразовать схему между узлами, если оставить потенциалы между точками преобразования.

Преобразование соединения в звезду и треугольник.

Найти токи в ветвях звезды и треугольника. Звезда – когда в узле сходятся три луча.

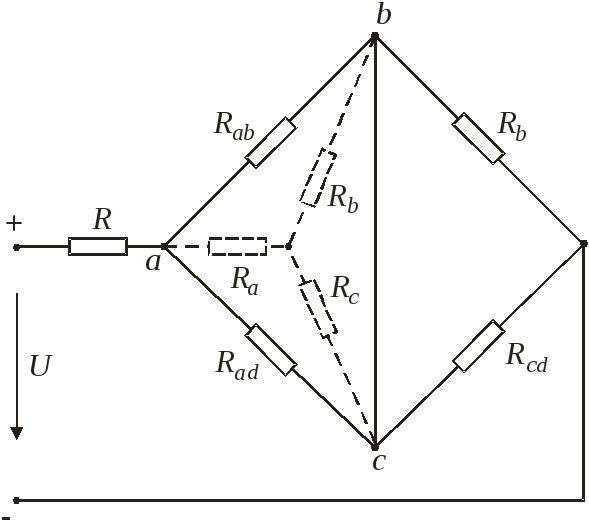
Если бы рассчитывали непосредственно по первому и второму закону Кирхгофа, то пришлось бы по первому закону Кирхгофа составить три уравнения и по второму закону Кирхгофа три уравнения.

Можно преобразовать схему, если оставим потенциалы: φa, φb, φc.

Получилась звезда с сопротивлениями Ra, Rb, Rc.

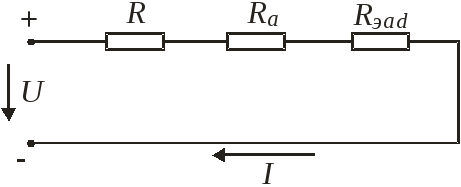
Таким же образом можно сопротивление звезды преобразовать в треугольники.

Линейные электрические цепи синусоидального переменного тока.

Синусоидальная - единственная форма тока, потому что косинус является производной от синуса. Это возможность использования уравнения Эйлера для расчета их применять комплексные числа.

Число полных изменений синусоиды за 1 секунду называется частотой переменного тока.

Время в течении которого синусоида полностью изменяется, называется периодом.

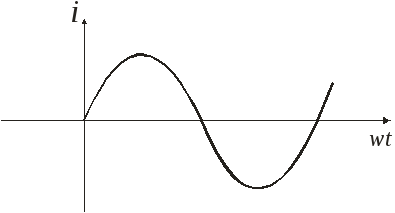
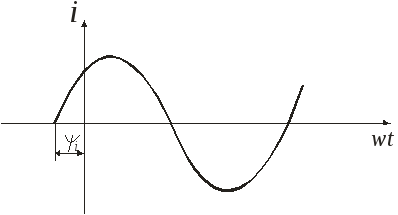
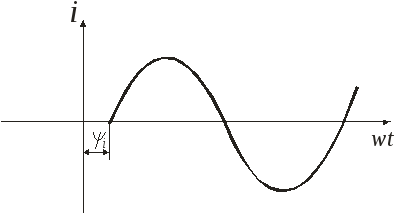
где I_m - максимальное, или амплитудное, значение тока,

- мгновенное значение тока i(t),

- угловая частота или скорость изменения аргумента функции,

- начальная фаза (аргумент функции в момент времени (момент включения), принятый за начало отсчета, т.е. при t = 0),

аргумент синусоидальной функции , называется фазой , и определяет значение функции i(t) в любой момент времени.

Условились, что какая-то величина переменного тока I, U, E будет равна какой-то величине постоянного тока, если у них будет одинаковая температура нагрева .

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока (среднеквадратичным значением тока за период или эффективным):

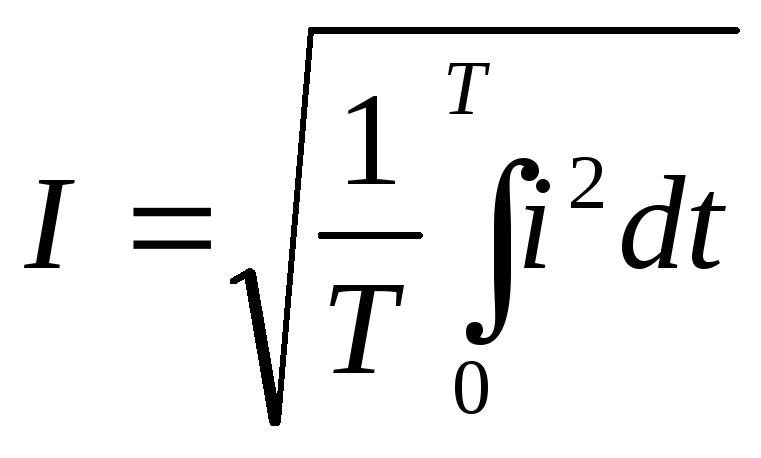
Аналогично определяются действующие значения ЭДС и напряжения.

Обозначим через I некоторый постоянный ток, при протекании которого по тому же участку цепи за время T выделится такое же количество тепла. Тогда с учетом того, что получим:

, аналогично , .

Подавляющее большинство приборов для измерения в цепях синусоидального переменного тока показывают именно эти действующие значения (тока I, напряжения U, ЭДС E).

Расчеты цепей переменного тока при включении активного, индуктивного и емкостного сопротивления (R, L, C).

В цепи переменного тока наблюдается эффект вытеснения тока в периферии сечения, у периферии больше, чем у центра. Но так как частоты низкие (50 Гц), то пренебрегаем этим явлением и считаем, что активное и омическое сопротивления одинаковы.

Активное сопротивление R в цепи синусоидального переменного тока.

Считается, что напряжение прикладывается сразу и достигает своего значения сразу.

Забегая вперед, напишем, что на участке с активным сопротивлением, ток повторяет функцию напряжения, совпадая с ним по фазе, на индуктивном сопротивлении всегда на этом участке ток начинается с нуля и отстает от напряжения на определенный угол, а на участке с емкостью напряжение на емкости начинается с нуля, а ток опережает это напряжение на определенный угол.

В цепях переменного тока доказывается положение о том, что уравнения и методы цепей постоянного тока могут быть записаны как для мгновенных значений, так для векторных и комплексных величин.

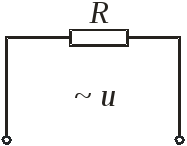
Сравниваем фазы напряжения и тока, видим их совпадения. На участке с активным сопротивлением ток и напряжение совпадают по фазе.

(Вт, кВт) – активная мощность в цепи с активным сопротивлением.

Индуктивность в цепи синусоидального переменного тока.

Положительное направление ЭДС совпадает с током. Т.к. магнитное поле собственное ЭДС самоиндукции.

При возрастании тока ЭДС самоиндукции направлена против тока, не дает ему увеличиваться, стабилизирует процесс.

Если

Действительное направление ЭДС совпадает с током, не давая ему исчезнуть.

Закон Ленца об ЭДС самоиндукции. Из схемы:

На участке с индуктивностью ток отстает по фазе от напряжения на угол 90° (π/2).

В правом уравнении ЭДС самоиндукции X_L – искусственно введенное реактивное сопротивление, которое заменяет собой действие ЭДС самоиндукции.

- закон Ома для участка с индуктивностью.

- реактивная мощность, вредная (Вар, кВар).

π / 2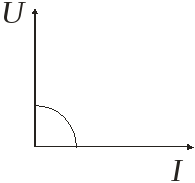

Емкость в цепи синусоидального переменного тока.

Емкость – два проводника, а между ними диэлектрик.

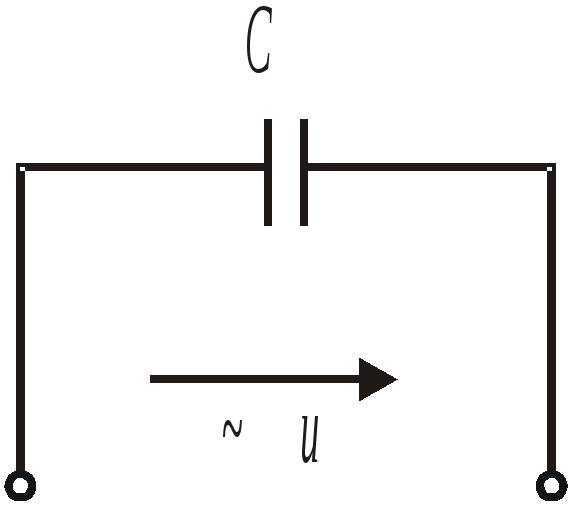
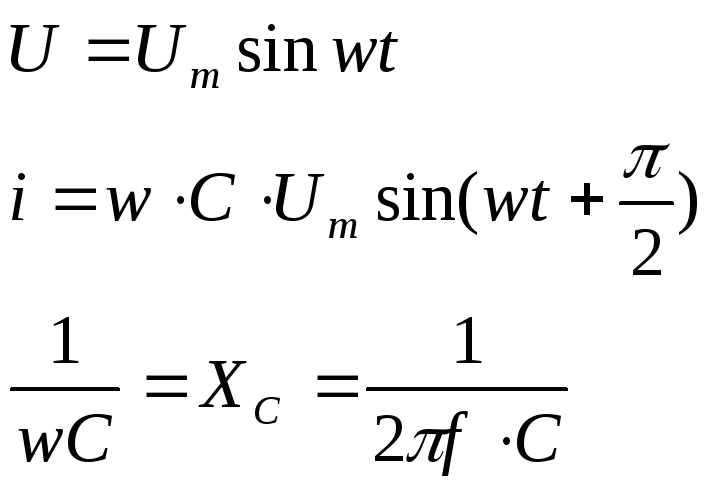
На участке с емкостью ток опережает приложенное к емкости напряжение на угол 90° (π/2). X_C – емкостное сопротивление.

- закон Ома для участка с емкостью.

- реактивная емкостная мощность (Вар, кВар).

π / 2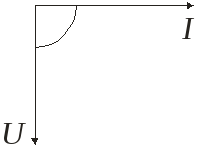

Из того, что ток на индуктивности отстает от напряжения, а на емкости опережает реактивная мощность индуктивности в любой момент времени находится в противофазе с емкостной, они стремятся друг друга уничтожить.

Последовательное соединение R, L, C.

для мгновенных значений -

для векторных значений -

для комплексных значений -

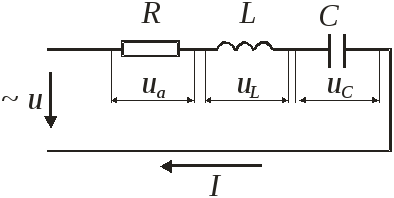
Целесообразно векторную диаграмму строить для общей для данного вида соединений величины. Для последовательного соединения целесообразно строить относительно тока, для параллельного – относительно напряжения.

Пусть характер цепи активно-индуктивный, т.е. ток отстает от напряжения на некоторый угол φ.

φ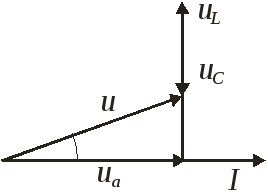

- модуль полного сопротивления цепи переменного тока.

- закон Ома для цепи переменного тока.

Модуль полного сопротивления в цепи переменного тока.

φ (Вт, кВт)

φ (Вар, кВар)

(ВА, кВА)

φ – какая часть производимой мощности идет на совершение полезной работы.

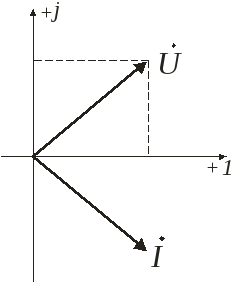
Символический метод или расчет цепей с применением комплексных чисел.

Диаграмму напряжений поместим на комплексную плоскость (), умножение на j есть поворот комплексного числа на 90° против часовой стрелки.

|e^jφ| = 1 =

Z – полное комплексное сопротивление цепи переменного тока.

- модуль комплексного сопротивления

До сих пор мы имели дело с модулем полного комплексного сопротивления .

- полная комплексная мощность – произведение комплекса напряжения на сопряженный комплекс тока.

Все электротехнические расчеты выполняются с помощью комплексных чисел. Применение комплексных чисел при расчете цепей синусоидального переменного тока позволяет перейти от геометрических операций над векторами к алгебраическим действиям над комплексными числами (алгебраически складываются действительные части с коэффициентами мнимой части комплексного числа). Поэтому все методы, законы, уравнения постоянного тока могут быть использованы в цепях переменного тока, но записанные с помощью комплексных чисел. Можно применять метод двух узлов, контурных токов и т.д.

Перед расчетом какой-либо цепи ее предварительно необходимо преобразовать в комплексной форме для применения символического метода.

В А

Вар

Пример 1: нагрузка чисто индуктивная.

Расчеты символическим методом производятся над действующими значениями токов и напряжений. Если имеется начальная фаза, то действующее значение равно 0,707 амплитудного, wt = 0, t = 0 и остается синус начальной фазы.

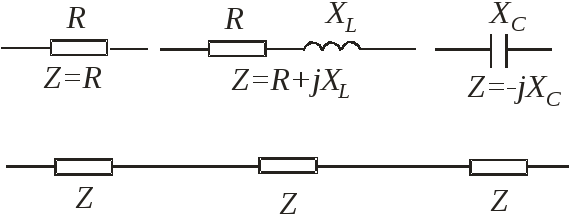
Перед расчетом необходимо реальную схему преобразовать в прямоугольники.

1)

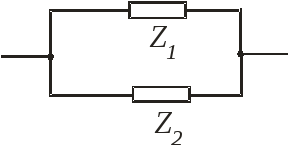
Резонансы в электрических цепях в.

При последовательном Х_L и Х_C (рис1) возможен последовательный резонанс напряжений. Если же Х_L и Х_C соединены параллельно (рис2), то может возникнуть параллельный резонанс, или резонанс токов.

Под резонансом электрических цепей понимают такое состояние, когда частоты свободных и вынужденных колебаний совпадают, ток и напряжения совпадают по фазе. Когда нагрузка становится чисто активной, потребляется чисто активная мощность, реактивная мощность равна 0, а полная мощность S = P.

Резонанс напряжений.

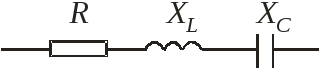
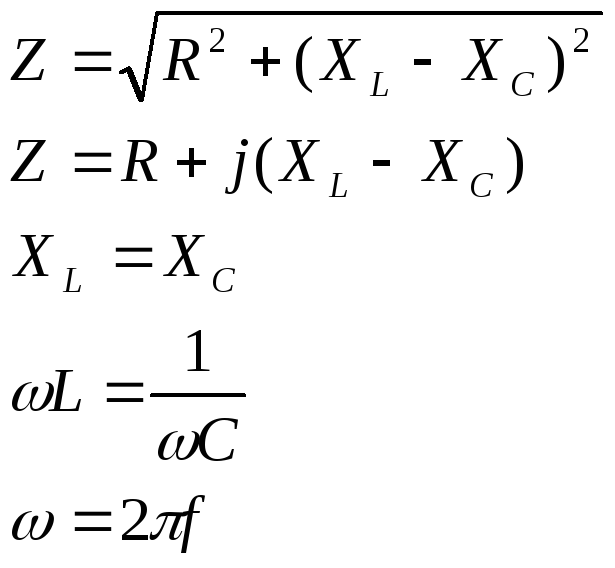
Резонанс напряжений, может быть, достигнут тремя путями:

1. Изменить частоту

2. Изменить индуктивность

3. Изменить емкость

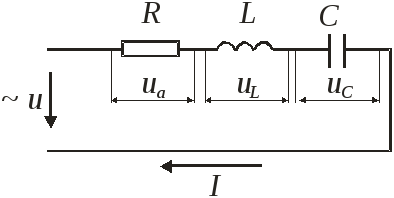
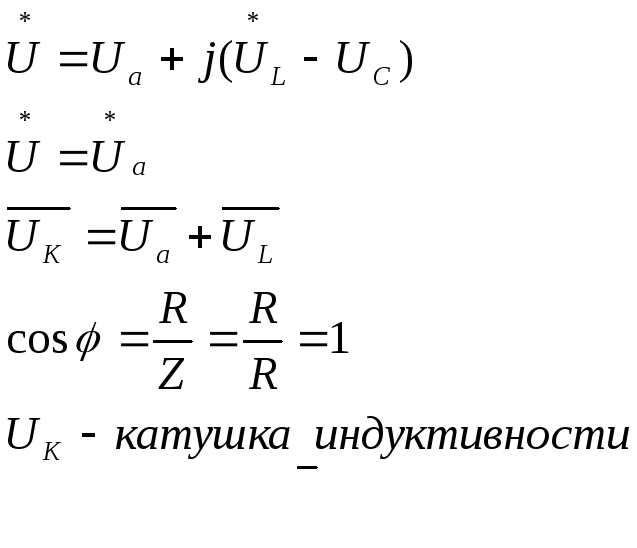
При резонансе напряжения, напряжения Х_L и Х_C находятся в противофазах, их разность равна 0. Но сами могут достигать значительных значений.

Q – добротность контура, показывающая во сколько раз напряжение на индуктивности и ли на емкости превышает напряжение в сети.

Резонанс напряжений вещь вредная, и его надо предусматривать.

При резонансе ток не только совпадает по фазе, но и достигает max-го значения.

Резонанс напряжения – это когда частоты вынужденных колебаний (сети) совпадают с колебаниями собственной частоты.

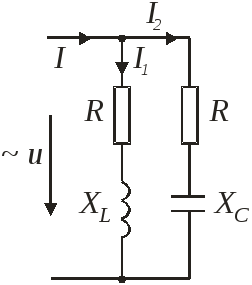
Резонанс токов. (или параллельный резонанс)

В этом случае может возникнуть в колебательном контуре резонанс токов, который характеризуется совпадением по фазе I и U в неразветвленной части коэффициент мощности равен 1. Когда отсутствует во внешней цепи реактивная мощность, а проводимость становится чисто активной и равная сумме активных проводимостей параллельных ветвей.

Общая проводимость

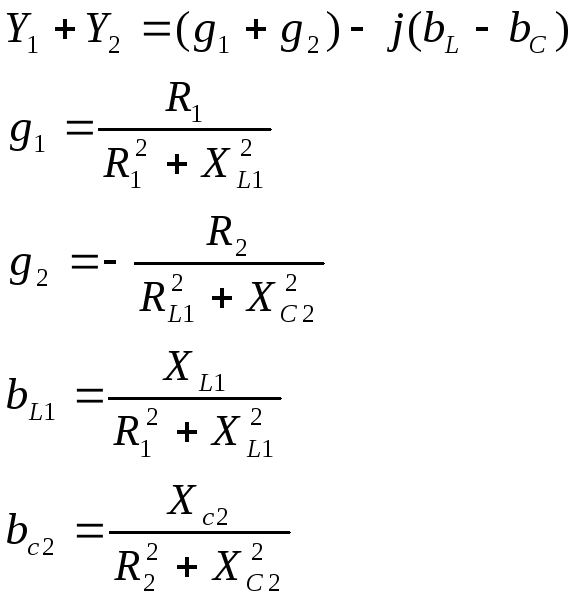
В цепи параллельного тока активная проводимость зависит так же от реактивного сопротивления:

1 X_L

2 X_C

Резонанс тока наступает, когда

Кроме того, резонансного тока можно добиться изменением частоты Х_L и Х_C , а так же активных сопротивлений этих ветвей.

При этом ток будет

Ток в неразветвленной части контура будет совпадать по фазе с общим напряжением.

По первому закону Кирхгофа

φ2

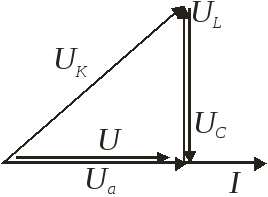
φ1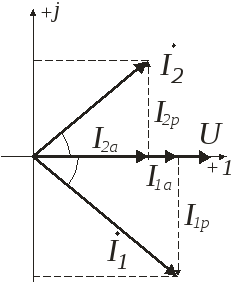

Из векторной диаграммы видно, что при резонансе тока реактивная составляющая индуктивного = реактивной составляющей емкостного и находятся с ней в противофазах.

Общий ток в неразветвленной фазе равен сумме активных составляющих токов 1 и 2 и совпадает по фазе с приложенными напряжениями.

Явление резонанса тока явление полезное и служит для искусственного увеличения , а следовательно к уменьшению реактивно-индуктивной мощности, а при их равенстве

Пример:

Пусть потребитель имеет активно-индуктивный характер.

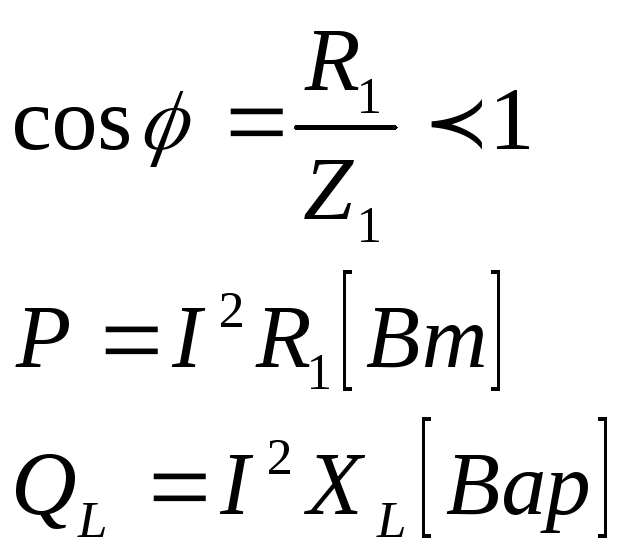
Нужна мощность, чтобы подключить еще один потребитель, тогда у нас будет

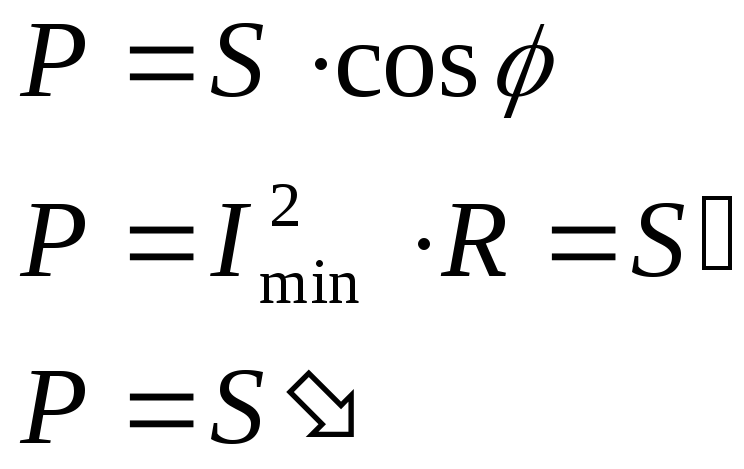
При этом из сети будет забираться чисто активная мощность меньше прежней S, то есть создается запас по мощности для подключения дополнительного потребителя.

Этот способ увеличения до 1 называется способом улучшения , способом получения чисто активной мощности.

Пример:

Дано (Комплексное) мгновенное выражение для тока.

i=50

Комплекс тока i=50А, начальная фаза запишем выражение мгновенного значения тока:

Трехфазные системы синусоидального тока.

Преимущество:

1) Возможность получения кругового вращающегося магнитного поля.

2) И поток, и магнитное поле постоянны в любой точке.

3) Минимальные потери при канализации этой системы.

4) Простота расчета.

Пример трехфазного асинхронного двигателя:

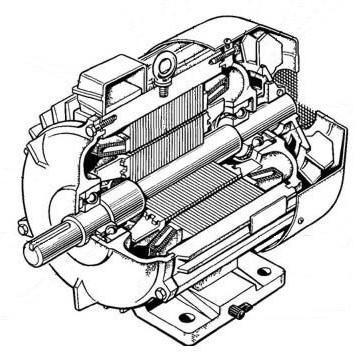
Схема трехфазного асинхронного двигателя:

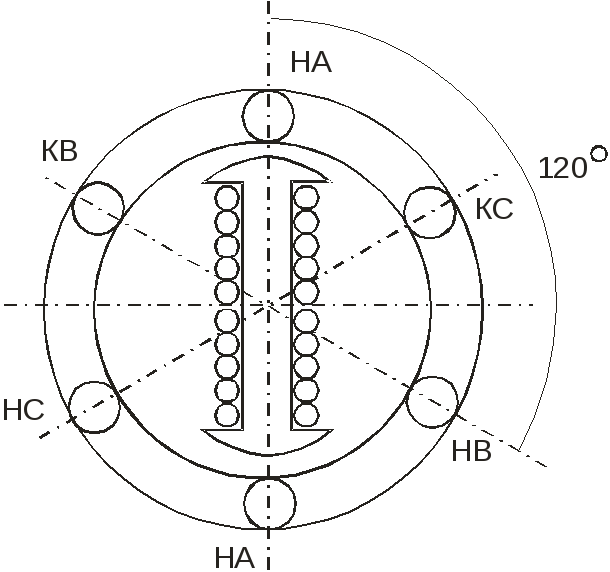
Обмотки статора сдвинуты на 120 градусов. В каждой обмотке при вращении индуктора отдельно наводится синусоидальная однофазная ЭДС, которая конструктивно сдвинута одна относительно другой на 120 градусов. А, Б, С – фазы.

e

e_A

e_B

e_C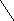

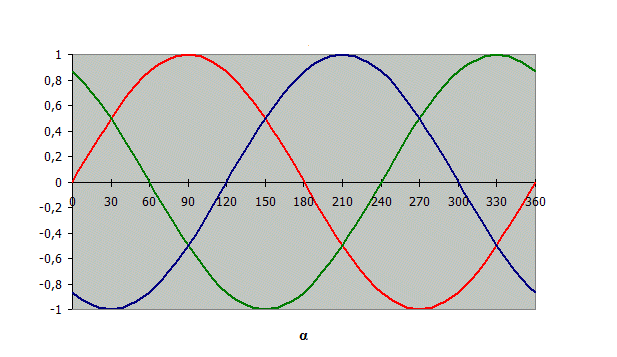_А, e_В, e_с. e_А + e_B + e_C. = 0

! Алгебраическая сумма ЭДС равна нулю в любой момент времени.

Это дает основание записать, как это было доказано в 1-фазном токе с помощью комплексных чисел для действующих значений комплексов:

Следовательно, под трехфазной системой ЭДС понимают три отдельных однофазных ЭДС одинаковой частоты, амплитуды, но сдвинутых на 120 градусов по отношению к друг другу. И если концы этих обмоток соединить в одну точку, то получим звезду фазных ЭДС.

Если последовательность достижения максимумов ЭДС АВСАВСАВС и т.д., то это прямая последовательность. Если последовательность АСВАСВАСВ и т.д. то это обратная последовательность.

При прямой последовательности получается круговое вращательное магнитное поле по часовой стрелке, при обратной - против часовой. Если изобразить 3-х фазную систему на комплексной поверхности, причем по оси действительных отложить направление А.