§ 6. Метод разделения переменных для параболических уравнений

Рассмотрим смешанную задачу для уравнения с переменными коэффициентами:

Предполагаем, что функции непрерывны на отрезке

и выполнены неравенства

Будем искать решение задачи (5658) в форме

(59)

и подставляя (59) в (56), после разделения переменных получим

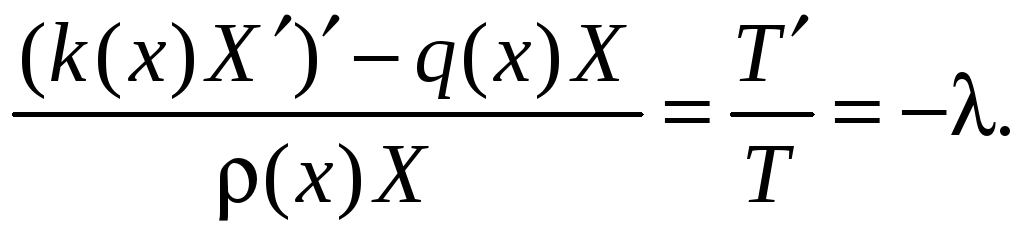(60)

Из (57) и (59) вытекает, что функция Х(х) должна удовлетворять гранич- ным условиям Присоединив эти граничные условия к дифференциальному уравнению для Х(х) получим, так называемую, зада- чу ШтурмаЛиувилля:

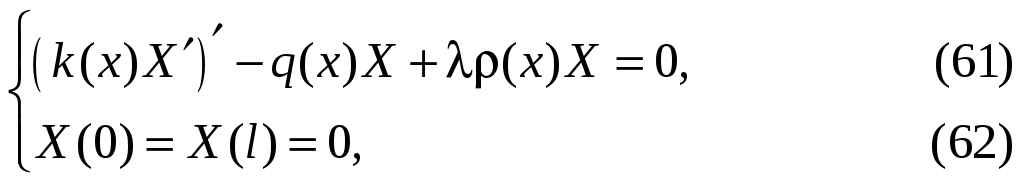
где нужно определить значения параметра и соответствующие нетри-

виальные решения Х(х).

Определение. Те значения параметра , для которых задача (61 62) имеет нетривиальные решения, называются собственными значениями, а соответствующие нетривиальные решения называются собственными функциями.

Ранее у нас встречалась задача ШтурмаЛиувилля (3738) для урав-нения с постоянными коэффициентами и нахождение ее собственных функций базировалось на возможности найти явно общее решение диф- ференциального уравнения. Теперь мы имеем такую ситуацию, когда уравнение (61), вообще говоря, не интегрируется в квадратурах и в первую очередь возникает вопрос о существовании собственных значений и собственных функций и их свойствах.

Справедливы следующие три теоремы.

Теорема 1. Задача ШтурмаЛиувилля (6162) имеет счетное множес- тво положительных собственных значений

отвечающие различным собственным значениям, взаимно ортогональны друг другу с весом на отрезке , т. е.

Теорема 3. Если f(x) имеет на непрерывные производные до вто- рого порядка включительно и удовлетворяет граничным условиям

то она разлагается в абсолютно и равномерно сходящий- ся ряд Фурье по собственным функциям задачи (6162)

где коэффициенты Фурье вычисляются по формулам

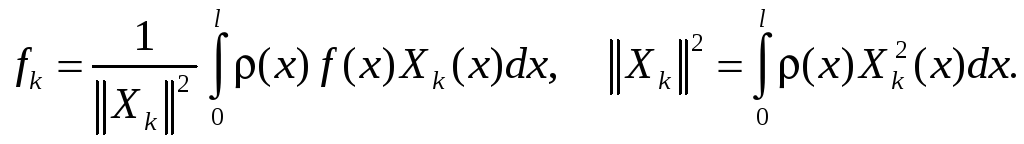
Считая задачу Штурма-Лиувилля решенной, вернемся к равенству (60) и решим дифференциальное уравнение

Очевидно, что Теперь составляем ряд

(63)

и определяем А_k так, чтобы выполнялось начальное условие (58), т. е.

откуда в силу теорем 2 и 3 следует, что

(64)

Итак найдено , что решение задачи (5658) дается формулами (63), (64).

Заметим, что теорема 2 об ортогональности будет иметь место и для других задач ШтурмаЛиувилля, если граничные условия (57) заменить на или, например, Более того, чуть позже рассмотрим так называемый особый случай, когда коэффи –циент k(х) обращается в нуль в точках х=0 и , и собственные функ- ции будут снова составлять ортогональную с весом ρ(х) систему функ- ций.

Разумеется, что рассмотренная задача ШтурмаЛиувилля для уране-ния с переменными коэффициентами может возникнуть и при решении уравнений гиперболического или эллиптического типа. Если, например,

в правой части (56) заменить на , то получим уравнение гипебо- лического типа с переменными коэффициентами, решение которого будет опираться на задачу (6162).

192. Имеется однородный тонкий стержень длиной , изолированный от окружающего пространства, с начальной температурой Определите температуру u(x,t) точек стержня при t>0, если концы стерж- ня поддерживаются при температуре, равной нулю.

Р е ш е н и е. Поставленная задача равносильна смешанной задаче

которую решаем методом Фурье, полагая После подстановки в дифференциальное уравнение и разделения переменных найдем

Из граничных условий получим

Теперь решаем задачу Штурма-Лиувилля:

Из дифференциального уравнения находим, что

и, следовательно, решение смешанной задачи будет иметь вид

Определим коэффициенты А_k так, чтобы выполнялось начальное условие

Подставляя значения коэффициентов в ряд, придем к ответу

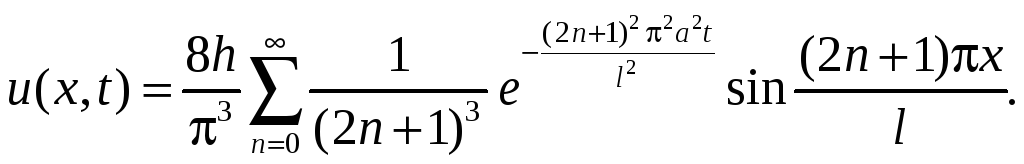
193. Растворенное вещество с начальной концентрацией u₀ диффундиру- ет из раствора, заключенного между плоскостями х=0 и в раствори- тель ограниченный плоскостями x=h и . Определить процесс вырав- нивания концентрации, предполагая, что границы х=0 и непроница- емы для вещества.