§ 3. Классификация и приведение к каноническому виду уравнений в частных производных второго порядка

Линейные относительно вторых производных уравнения

(21)

где и произвольная функция пяти переменных, относятся к одному из трех типов в зависимости от знака дискриминанта

(22)

Если дискриминант D>0, то уравнение (21) называется уравнением ги-

перболического типа; если D<0, то уравнение (21) называется уравнени-

ем эллиптического типа; если дискриминант D=0, то уравнение (21) называется уравнением параболического типа.

По левой части (21) составляется уравнение характеристик

(23)

Если D>0, то уравнение (23) распадается на два обыкновенных дифе- ренциальных уравнения первого порядка, и при их решении получим два общих интеграла

(24)

Их левые части нужно брать в качестве новых переменных

относительно которых получим каноническое уравнение

(25)

Если D<0, то левые части соотношений (4), будут комплексно-сопряженными и в качестве новых переменных выбирают

Соответственно придем к каноническому уравнению эллиптического типа

(26)

В параболическом случае, когда D=0, уравнение характеристик сводится к одному уравнению, соответственно получится один общий интеграл

(24^/)

Вводятся новые переменные , где в качестве второй переменной берется любая функция функционально независимая от В итоге придем к каноническому параболическому уравнению

(27)

Будем рассматривать линейные уравнения в частных производных

2-го порядка

(28)

где суть функции от независимых переменных

На этот раз тип уравнения (28) можно определить только для фиксированной точки

по левой части уравнения, точнее по коэффициентам

путем введения новых переменных

(29)

Относительно новых переменных придем к уравнению

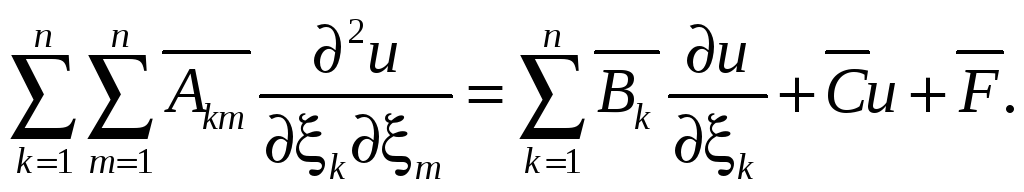(28^/)

Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ эллиптичес- кий тип, если существует невырожденное преобразование вида (29) та- кое, что в уравнении (28^/) при , при

Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ гиперболичес- кий тип, если существует невырожденное преобразование вида (29) та- кое, что в уравнении (28^/) при а среди коэффициентов имеется v коэффициентов, равных единице, и n-v коэффициентов, равных минус-единице.

Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ параболический тип, если существует невырожденное преобразование вида (29) такое, что в уравнении (28^/) при , а среди коэффициентов наряду с единицами и минус-единицами также имеются нули.

Если в уравнении (28) коэффициенты левой части A_ij постоянные, то из приведенных определений ясно, что это уравнение будет иметь один и тот же тип во всем n-мерном пространстве.

122. Приведите к каноническому виду уравнение

Р е ш е н и е. Дискриминант т. е. уравнение имеет гиперболический тип. Уравнение характеристик

распадается на два уравнения

Вводим новые переменные тогда

Подставляя найденные производные в исходное уравнение, получим

123. Приведите к каноническому виду уравнение

Р е ш е н и е. Дискриминант т.е. уравнение имеет

эллиптический тип. Уравнение характеристик

распадается на два дифференциальных уравнения с комплексно сопряженными правыми частями. Решаем одно из них

Вводим новые переменные, полагая тогда

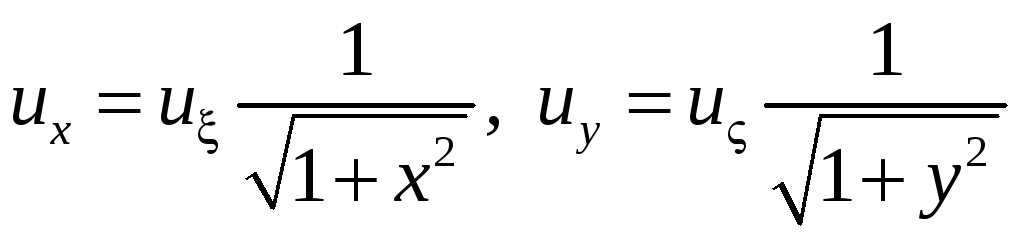
Подставляя найденные производные в исходное уравнение будем иметь

124. Приведите к каноническому виду уравнение

Р е ш е н и е. Дискриминант т.е. уравнение имеет параболический тип. Уравнение характеристик

имеет один общий интеграл

Вводим новые переменные Тогда

Подставляя найденные производные в исходное уравнение, получим

125. Приведите к каноническому виду уравнение

(30)

Рассмотрим квадратичную форму

По методу Лагранжа ее можно записать в форме

Полагая получим относительно но- вых переменных квадратичную форму

и это означает, что дифференциальное уравнение имеет эллиптический тип и приводится к виду

(30^/)

с помощью линейной замены. Для ее нахождения выразим переменные через переменные так, что

или в матричной форме

Теперь нужно взять транспонированную матрицу и использовать равенство

,

или в скалярной форме

Определите тип и приведите к каноническому виду следующие уравнения второго порядка:

126.

127.

128.

129.

130.

131.

132.

133.

134.

135.

136.

137.

138.

139.

140.

141.

142.

143.