15.Линейная регрессия.
1). Выборочная линейная среднеквадратическая регрессия.
Линейная регрессия является простейшей регрессионной моделью, согласно которой функция регрессии является линейной 2-параметрической функцией:
,
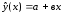где
-
неопределенные коэффициенты, которые
оценим по наблюдаемым данным. Пусть
имеется двухфакторная выборка наблюдений
объема n
за величинами X
и Y,
будем называть корреляционным полем.
Помимо выборочных средних значений
и выборочных дисперсий
,
вычислим так же среднее произведение
и выборочный (эмпирический) коэффициент
корреляции
,
который является выборочным аналогом
теоретического коэффициента корреляции
Пирсона
.
Построим оценки
коэффициентов
методом наименьших квадратов. Для этого
найдем такие значения
,
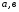которые минимизируют сумму квадратов
отклонения
и
,
то есть ошибок
.
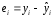
Из необходимых
условий минимума найдем искомые оценки
:
;
;
,
;
;
.
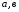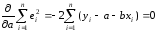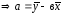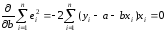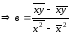Через выборочный
коэффициент корреляции
,
коэффициент
представим в форме
,
а уравнение выборочной линейной
среднеквадратической регрессии имеет
одну из следующих форм:
;
;
;
.