1Случайное событие. Частота события.

Определение. Событие – исход некоторого опыта.

Определение. Случайное событие – то, что может произойти либо не произойти.

Естественнее всего их характеризовать следующим понятием.

Определение. Относительной частотой 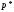случайного события называется отношение числа появления данного события к общему числу проведённых испытаний, в каждом из которых может появиться или нет данное событие:

.

Чаще всего оказывается (по крайней мере, теория вероятностей имеет дело именно с такими частотами, а иные ситуации в ней не рассматриваются), что:

,

где 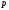- некоторое число.

Определение. Такое число называется вероятностью появления случайного события .

2.Классификация случайных событий: несовместные и совместные события, достоверные и невозможные события, равновозможные события, противоположные события. Полная группа событий. Классический способ вычисления вероятности.

Определение. Два события называются несовместными, если наступление одного из них исключает возможность наступления другого. В противоположном случае события называются совместными

Определение. События называются равновозможными (равновероятными), если вероятность наступления каждого из них одна и та же.

Определение. События образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное (отличное от входящих в группу) событие.

Определение. Событие называется достоверным, если оно не может не произойти в условиях данного опыта.

Вероятность достоверного события равна 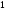, т.к. для этого события (напомним, что ).

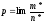Определение. Событие, которое не может произойти в условиях данного опыта, называется невозможным событием.

Вероятность невозможного события равна , т.к. для этого события (а ).

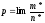Пусть мы имеем полную группу равновозможных, несовместных, случайных событий.

Определение. Событие (из такой группы) называется благоприятствующим появлению события , если появление этого события (из такой группы) влечёт за собой появление события .

Классический способ нахождения вероятности

Вероятность события равна отношению числа 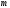благоприятствующих случайных событий к числу всех возможных случайных событий , образующих полную группу равновозможных несовместных событий:

.

Исходя из приведённого правила, можно опять установить, что для событий, имеющих полную группу равновозможных несовместных событий, имеет место два свойства вероятности:

,

.

3. Необходимые сведения из комбинаторики. Их использование при решении задач теории вероятности

Числом размещений называется частное от деления:

.

Оно представляет собой число всех возможных комбинаций из чисел, расставленных по местам, при этом порядок, занимаемый числами, имеет существенное значение.

Числом сочетаний из элементов по элементам называется число

,

обозначающее число способов, которыми можно расположить чисел по местам (при этом порядок, занимаемый числами, не имеет значения).

4.Теорема сложения вероятнорстей(для независимых и зависимых событий)

Вероятность суммы совместных событий и равна:

.

Вероятность суммы несовместных событий 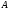и равна:

.
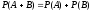